
水鉄砲の穴をめぐって 本稿は【物理教育通信 第96号(1999/05)掲載記事(PDF737KB)】のリライト版です。
神奈川県立湘南台高校・YPC(横浜物理サークル) 山本明利
1.話の発端
98/10/12にNHK「やってみようなんでも実験」で放送された、「水鉄砲は穴が小さいほどよく飛ぶ」理由の解説はおかしいのではないかという話題(10/17の再放送では当該シーンは訂正されていた。)がきっかけとなり、YPC(横浜物理サークル)の'98年10月例会では、水を満たした容器の同じ高さのところに大小の穴をあけ、水を水平方向に噴出させたら、どちらの穴から出た水が遠くへ飛ぶかという実験が行なわれた。圧力が同じだから飛距離は等しいと思いきや、大きい穴の方が飛距離が大きいという結果だった。
その理由については、例会の席で右近修治氏の解説があり、一同、一応は納得したのである。実験の模様と右近氏の解説は、物理教育通信No.95,P.97の資料紹介で報告されている。しかしその後、YPCメーリングリストで高橋和光氏から問題の再提起があったため、この件について再点検し、整理をしてみた。
2.水鉄砲の理論(グレアムの法則)
まず、話のきっかけとなった水鉄砲について考える。無重力のもとで密度ρの粘性のない非圧縮性流体が十分大きなシリンダーに入れられ、ピストンで与圧されているとする。シリンダーの先端の穴から噴出する流体の速度をv、シリンダー内外の圧力をそれぞれP1、P0とすると、ベルヌーイの定理により、
![]()
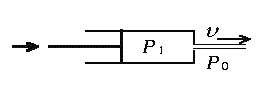
が成り立ち、
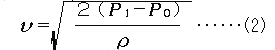
を得る。つまり水鉄砲の噴流の流速は内外の圧力差のみによって決まり、穴の大きさによらない。これをグレアムの法則というのだそうだ。
3.トリチェリの定理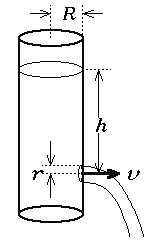
次に、YPC例会で行なわれた実験の考察にうつる。 半径Rの円筒型の容器の薄い壁に、半径rの円形の穴を あけ、穴の位置から測って高さhのところまで、密度ρ の液体が入っているものとする。重力による圧力差で穴 からは速さvで液体が噴出する。粘性のない非圧縮性流 体を考えると、ベルヌーイの定理により
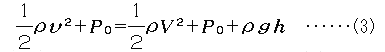
が成り立つ。ここにP0は周囲の大気圧、Vは容器内の液面の降下する速さである。大気圧の差は無視してよ いので、整理して
![]()
を得、さらに容器が十分大きくてVが無視できる場合には、次式を得る。
![]()
これを仮に理想流速と呼ぶことにする。理想流速は質点が液面から穴まで自由落下したときに得る速さに等しい。これをトリチェリの定理と呼ぶこともあるらしい。
4.右近理論とその限界
次に、右近氏の解説を復習する。流体の連続性を考えると、流下した体積と噴出した体積は等しくなければならないので、
![]()
が成り立つ。これをVについて解いたものを(4)式に代入して整理すると、次式を得る。
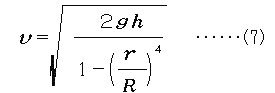
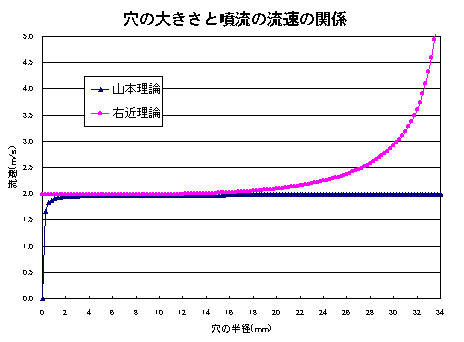
これを右近式と呼ぶことにする。右近式によると穴の半径rが大きいほどvが大きくなることが示され、Rがrに比べて十分大きい場合には(5)の理想流速に一致するので、定性的には実験の結果を説明しているように見える。
しかし、右近式には穴を大きくしていった場合に明らかな限界がある。rがRに近づくにつれ、vは急速に増大し、発散してしまうのである。容器内の流体が加速度運動をしてしまうような条件のもとではこの式は使えない。
5.表面張力からのアプローチ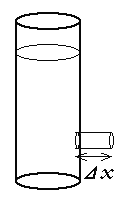
つぎにちょっと視点を変えて、噴出した流体の部分の 表面の自由エネルギーを増すための仕事という観点から アプローチできないかと考えてみた。やはり(3)〜(5)式 をベースに考えることにする。
半径rの穴から水柱がΔxだけ押し出されたときをイ メージして、体積πr2Δxを(4)の両辺にかける。この のエネルギー保存の式において、2πrΔxという円柱 の表面を新たに形成するために行われる仕事2πrΔxσ (ここにσは水の表面張力)を考慮し、Rがrに比べて十分大きい(Vが無視できる)ものとして
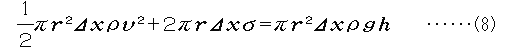
という式をたててvについて解くと、
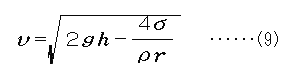
となる。これを仮に山本式と呼ぶことにする。山本式ではやはりrが大きいほど流速vが大であるという結果が導かれる。さらにrが十分大きいとき理想流速に一致するという結果となり、右近式の発散の困難を解決して、リーズナブルであるように感じられる。しかし、やはりベルヌーイの定理から出発しているので、あくまでも定常流が前提となっていることに変わりはない。山本式は容器の半径Rを含まないが、Rはrに比べてかなり大きい場合に適用されると考えるべきだと思う。
右近式と山本式のr依存性のちがいをグラフにして示すと図1のようになる。グラフの計算にあたっては、ρやσは常温における水の値を用い、後述する実験の条件に合わせて、容器の半径Rは3.5cm、水位hは20cmとした。穴の半径が20mmより大きいときと、1mmより小さいときに両者の差が顕著になる。
6.しきい水位
山本式(9)では、根号内の第2項が2ghよりも大きくなるとvは虚数になってしまう。液体が流出して水位hが下がると、いずれこの困難に直面することになる。この解決策を考えよう。式(9)は次のように変形できる。
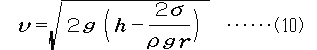
このとき()内の第二項 2σ/ρgr は、半径がrの穴から水が漏らないしきい水位h0を与えるものと考えられる。つまり、表面張力に打ち勝って穴から出るには穴の径に応じた圧力差が必要で、これだけの水柱の高さに相当する圧力をロスしてしまうので、その分をhから差し引いて考えよ、という意味に解釈できる。
7.「水ももらさぬ」穴
上の考察とは逆に、水位hを固定しておいて穴を小さくしていくと、表面張力のため水が出なくなる限界がある。その半径をr0とするとラプラス・ヤングの式から
![]()
が成り立つ。右辺が表面張力による圧力差を表す。これから
![]()
となる。水位hに対して、穴の半径が上式で与えられる大きさ以下だと液体はこぼれないというわけである。
さて、式(12)がrの下限であれば、式(9)で
![]()
なので、必ず
![]()
となり、まことに好ましい結果に見える。これでよければ、穴の径による噴流の流速の違いは主として表面張力による効果であると結論できるのだが・・・。
8.測定結果はいかに
どんなに美しい理論も現実との一致がなければ画餅にすぎない。理論の妥当性を検証するのはやはり実験によるべきだろう。試みに、液体として水を考え、その表面張力σ=73×10-3N/m(常温)、水の密度ρ=103kg/m3を代入すると
![]()
となる。水位をh=0.2mとすると、r0=0.074mmとなり、穴の径がこれ以下だと水は流出しないことになる。逆に穴の径を決めて、しきい水位を観測することもできる。r=0.5mmに対し、上式よりh0=約3cmとなる。実験としては後者の方が簡単である。ドリルでPETボトルに直径1mmの穴をあける。水を満たして水を噴出させ、そのまま放置して、どの水位で流出が止まるかを観察すればよいのである。
しかし、残念ながら実験は失敗だった。予想される3cmに近づくにつれ流出速度は限りなく0に近づいていくのだが、最終的に水流はPETボトルの壁をつたう形になり、一種の毛管現象で流出が続くのである。水がある程度PETを「濡らす」ことによる現象と思われる。容器の底に直径1mmの穴をあけ、水を流下した場合も、確かに水の流出は途中で止まるが、そのときの水位は予想されるh0の半分ほどになる。
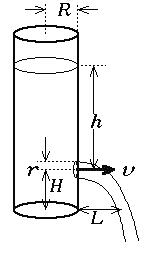 そこで次に、水位hに対する流速vの変化を連続的に測定してみることにした。テニスボールの空き缶(R=3.5cm)の底から高さH=2.5cmのところにr=0.5mmの穴をあけ、水を流出させながら水位hと水平到達距離Lの関係を測定した。本当は連続した噴流は粘性のため懸垂線(カテナリ)を形成するはずだが、水平投射と見てLを
そこで次に、水位hに対する流速vの変化を連続的に測定してみることにした。テニスボールの空き缶(R=3.5cm)の底から高さH=2.5cmのところにr=0.5mmの穴をあけ、水を流出させながら水位hと水平到達距離Lの関係を測定した。本当は連続した噴流は粘性のため懸垂線(カテナリ)を形成するはずだが、水平投射と見てLを
![]()
で割った値をvの測定値とした。
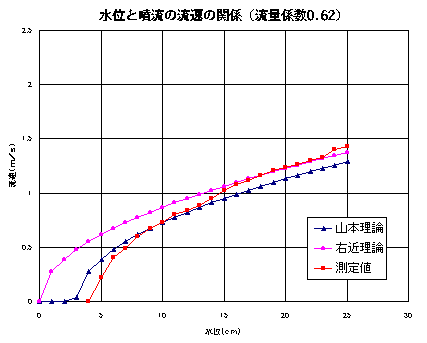
水の場合の測定結果と式(7)および(9)の計算値の比較 を図2に示す。どちらの式も測定値との一致はよいとは 言えない。しきい水位の存在は山本式に分があるが、曲線全体の形はむしろ右近式に近いとも言える。
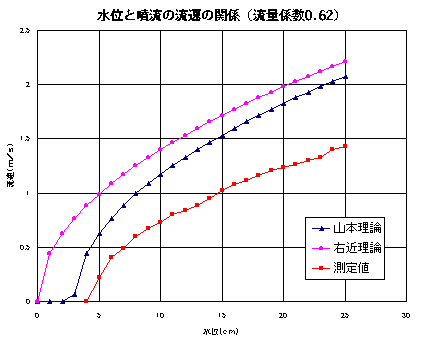
試みに、オリフィス(薄い板にあけた鋭い円形の穴)の経験的流量係数0.62を上記の計算値にかけてみたものが図3である。確かに一致はよくなるが、曲線の傾向が若干異なるようだ。流量係数がどのようにして決まるのかは不勉強でまだよく知らない。
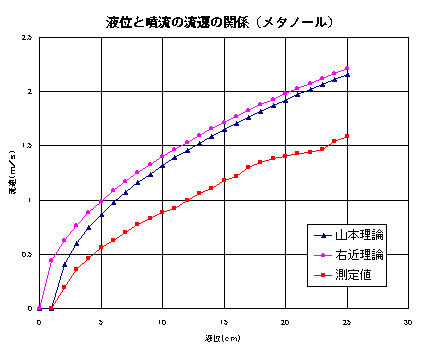
表面張力や密度の異なる液体について比較するため、メタノールによる測定も試みた(図4)が、やはりしき い水位の存在以外はよい一致とは言えない。
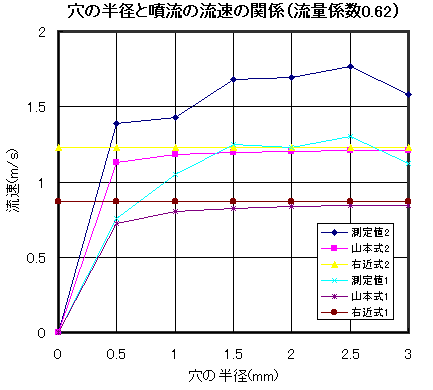
さらに、水について、穴の大きさを変えて噴流の流速を測定し、右近式、山本式との比較を試みたのが図5である。理論値にはそれぞれ流量係数0.62がかけてある。測定値1は水位h=10cm、測定値2は水位h=20cmのときのものである。いかにラフな測定とはいえ、両理論とも測定値との差は埋めがたいものがある。穴の半径r=0.5mmの値を見ると、図3で流量係数をかけたときの一致は偶然に過ぎなかったことがわかる。
9.今後の展望
右近式と山本式の融合は可能である。両者の条件は排他的ではないから、一つの式にまとめることはできる。容器の大きさに対して穴が小さい範囲ではそれで正しいはずだが、それでも理論値と測定値の大幅なずれの問題は解決しない。
YPC例会の席で井上賢氏から、「噴流は穴を出た直後にすでに乱流になっているはずで、そこでエネルギーをロスしているのだ。」とのコメントをいただいた。穴の出口で流れが縮む縮脈という現象も起こるらしい。さらに勉強してみたいと思う。
今は高等学校では教えなくなってしまった流体力学も、身近で大切な物理学である。これが教程に復活する日はもう来ないのだろうか。水鉄砲に端を発したこの話題も意外と奥が深くて面白い。課題研究の題材にいかがだろうか。
【参考文献】
YPCニュースNo.128('98/11/07)
戸田盛和「流体力学30講」朝倉書店(1994)
「理化学辞典第4版」岩波書店
本稿は【物理教育通信 第96号(1999/05)掲載記事(PDF737KB)】のリライト版です。