平成13年度新教科「情報」現職教員等講習会:モデル化とシミュレーション教材例
モホロビチッチ不連続面の発見
神奈川県立湘南台高等学校 山本明利

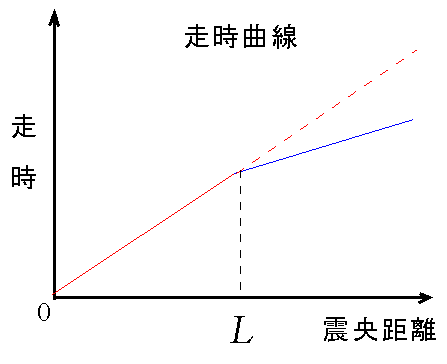
1909年、ユーゴスラビアの地震学者、モホロビチッチは、震源の浅い地震の走時曲線(震央から観測点までの距離を横軸に、地震波到達時間を縦軸にとったグラフ)が単純な直線にならず、右の図のように折れ曲がることを発見しました。
これは、震央から遠い観測点での走時は、地震波が観測点までやってくるのにかかる時間が距離に比例するものとして期待される時間(図の赤い破線部分)より短いことを意味します。何らかの経路で先回りしてくる地震波があるのです。
モホロビチッチは次のように推理しました。
すなわち、地震波速度の比較的遅い上部層(今では地殻と呼ばれている)の下に、地震波速度がより速い下部層(今ではマントルと呼ばれている)があり、遠隔地では後者を通った地震波が距離的には遠回りでも時間的には早く到達する、というものです。この発見により、地殻・マントル境界面はモホロビチッチ不連続面と呼ばれることになりました。
たとえて言えば、車で外出するのに最短距離の一般道と、距離的には不利な高速道のいずれを使うのが有利かは、目的地までの距離によって異なり、ある距離以遠では後者が有利になるということです。日常よく経験することですね。
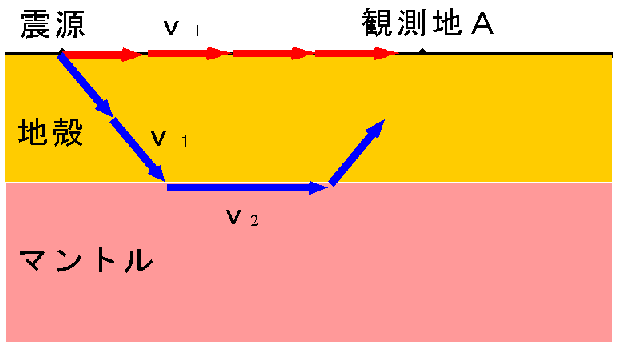
図で説明しましょう。赤い矢印は震源からストレートに地殻を伝わってくる遅い波です。こちらを直接波と呼ぶことにします。青い矢印は同じ速さv1でマントルへ向かい、境界面で屈折してより速い速度v2でマントル上部を進みながらたえず上方に波を送り出す、ヘッドウェイブという波です。こちらの経路をたどる波は屈折波と呼ぶことにします。下の図では観測地が比較的近いため、直接波が有利で赤矢印が先に到達することになります。
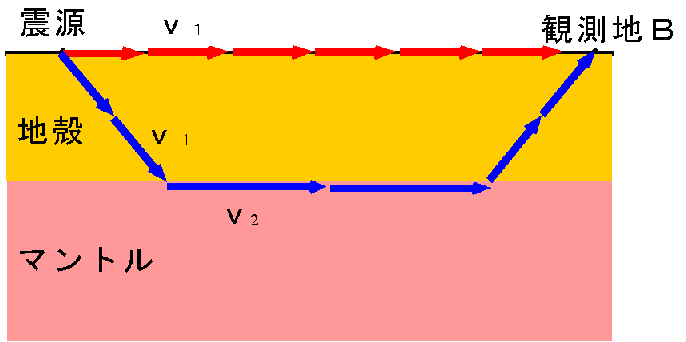
しかし、下の図のように観測地が震源から遠いと、屈折波の方が距離的には遠回りでも、時間的には有利になり、赤矢印より先に到達します。これがグラフの折れ曲がりの原因だったと考えられます。
両者が同時に到達する「引き分け」の地点が、グラフの折れ曲がりの場所になりますが、下の図のように、この地点の震央距離をL、地殻の厚さをdとしてLからdを求める方法を考えてみましょう。
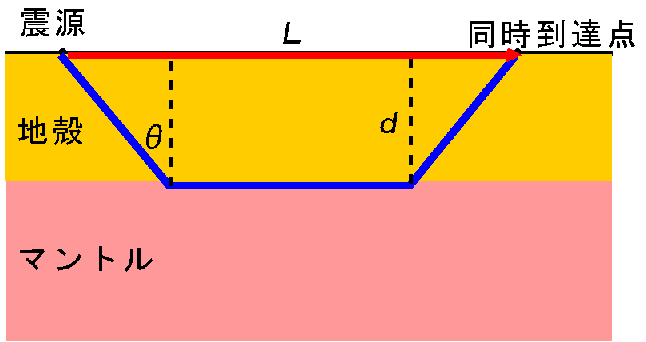
そのためには図の角度θが下の式を満たすことを使います。これは屈折の法則から導かれる臨界角の式です。v1、v2は前述のように、それぞれ地殻中、マントル中の地震波速度です。
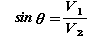
あとは幾何学の問題になります。下記の関係式が導かれるはずですので、やってみてください。
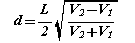
しかし、計算はけっこう面倒なので、この式の導出を地学の授業でやったら、いっぺんで嫌われてしまいます。そこで、表計算を使ったシミュレーションにより、実際の観測値にフィットするパラメータを決定することを考えてみましょう。これによりv1、v2、dという3つの未知量が決定できます。生徒は試行錯誤の中で、各パラメータがグラフのどの部分に反映しているかをつかむはずです。
ここをクリックしてmoho.xlsを開き、さっそくやってみましょう。(MS-Excelが必要です)
v1が折れ線の左側部分の傾きの逆数に、v2が折れ線の右側部分の傾きの逆数に対応しています。これらが決まれば、折れ曲がり点の位置はdによって変わります。v1→v2→dの順にパラメータを決定していくと近道です。