U−CASの物理 (PDF版693KB)
横浜物理サークル・山本 明利
《U−CASを浮かす》
U−CAS(ユーカス)は94年秋頃からちょっと話題になったおもちゃです。 しゃれたデザインの銀色のコマが中空に浮いて回転するもので、黒い台の上に数 センチ浮遊して、ふらつきながらも回転を続ける光景はとてもマジカルで、初め て見る人を驚かせずにはおきません。発売元は増田屋コーポレーション(Tel.0 3−3861−0151代)で、玩具店、デパート等で入手できます。 浮遊させるにはコツがあって、なかなか一筋縄ではいかないのですが、ポイン トはコマの重量(調整用のウエイトが付属している)と台の水平(調整用のくさ び付き)で、特に前者が極めて微妙です。安定条件さえつかめば、同じ条件下で は比較的楽に浮くようになります。浮遊の原理が磁気力であることは容易にわか ります。台もコマも強力な磁石です。磁場の目に見えない「ポテンシャルのくぼ み」にコマをのせるのです。 さて、年開け早々、通信ネット・NIFTY-Serveの教育実践フォーラムFKYOIKUの 「理科の部屋」で、このU−CASの話題を持ち出したところ、たいへん盛り上 がり、全国の理科の先生方がその構造解明と浮遊の原理の究明に乗り出しました。 以下はそこでの議論を通じて明らかになったU−CASの「秘密」です。

《U−CASの磁場》
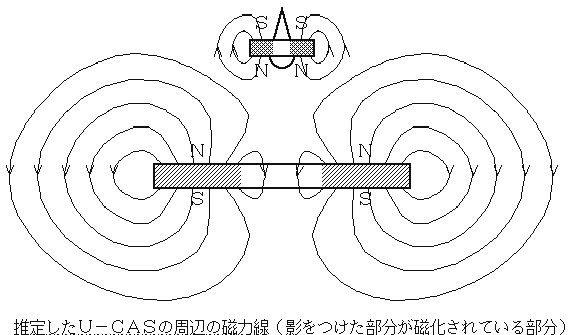
台(ベース)の周囲を棒磁石などで探ってみるとすぐにわかるのは、台の磁場 は中央で弱く、周辺部で強いこと。ドーナツ状に磁極が分布しています。極性は 上がN極、下がS極です。コマはこの逆の極性です。このことから、私はすぐに フェライトの大型リング磁石を連想し、これが台の中に埋めてあるものと推測し ましたが・・・真相はあとのお楽しみ。 「理科の部屋」の総力を上げたリサーチの結果、U−CASの台の周辺の磁力 線は上の図のようになっているらしいという結論に達しました。コマを持ち上げ ていくと、すっと浮き上がる点があることから、中央の上部には磁力線がくびれ ているところがあり、コマはこのくびれの上に浮くと考えられます。 U−CASの調整の最重要ポイントはバランスウェイトによる重量の加減です が、重すぎるとこのくぼみの下の「穴」に吸い込まれてしまい、軽すぎるとくぼ みが浅いので、不安定になってはじき出されてしまいます。うまくはまり込んで しかも墜落しない範囲はごくわずか(±0.05g程度)しかないようです。
《U−CASの構造》
ここまでは外から手探りで、目には見えない内部構造や磁場の様子を推定して きました。しかし、真相を知るにはやはり分解が近道。 まずコマの方の構造ですが、中に入っていたのは外径28.6mm、内径(穴の直径) 10.0mm、厚さ4.8mmのフェライトリング磁石です。N極を下にして組み立てられ ています。あとはプラスチックの外装(下の部分に磁石をすっぽりはめ、上の部 分でふたを被せる感じ)だけで、何も仕掛けはありませんでした。 一方、台(ベース)の方は、少々乱暴にこじ開けることになりました。中には ドーナツ状のリング磁石が・・・と思いきや、意外や意外、正方形の磁石が入っ ていました。中央には穴はあいていません。台の外装より一回り小さいだけの、 一辺10cm、厚さ1.2cmの正方形のフェライト板磁石です。ちょうど3.5インチのフ ロッピーディスクが入っているプラスチックケースを厚くしたぐらいです。それ が外周部だけ幅2cmほどずつ磁化されているのです。したがって、磁極の分布 は円形ではなく「角がやや丸くなった正方形」です。中央付近も同じフェライト が続いていますが、強くは磁化されていません。こんな磁石を今まで見たことが なかったもので、これはまったく予想できませんでした。
《U−CASの自作》
予想は大きく裏切られたものの、磁場の構造に関しては前記の議論は大筋で合 っているようなので、これだけの単純な構造なら、他の磁石を使っても浮くだろ う、というのが次なる挑戦です。 まず、手許にあった強力な大型フェライトリング磁石(外径90mm、内径40mm、 厚さ13mm)上でU−CASオリジナルのコマを浮遊させる試みです。残念ながら リング磁石1個では磁場が弱くて浮上に至りませんでした。おもりを全部はずし てもコマが重すぎるのです。ところが、同じ磁石を2個重ねてみたところ、がぜ ん磁場が強くなり、今度はおもりを追加しなければならないほどになりました。 ほとんどのおもりを装着して(総計約8g分)U−CASの銀色のコマは、むき出 しの2枚重ねフェライトリング磁石の上に静かに浮いたのです。浮上させるまで は、磁気力が強いためコマが暴れて少し難しいのですが、浮上してしまえば、こ ちらの方が軸のブレも小さく、安定した感じで浮きます。メーカーがなぜ「四角 い磁石」を選んだのか知りたい気もします。
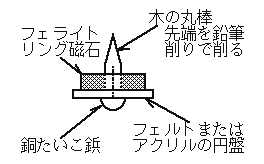

次はコマの自作です。試作したコマの材料は下記の表のとおりで、横浜の東急 ハンズ等で購入しました。作り方はインテリアフェルトまたはアクリル円盤の中 央にたいこ鋲をさし、反対側から木の丸棒をとりつけてコマの軸とします。たい こ鋲の頭がコマの足になります。円盤はボール紙でも何でもよいのですが、加工 しなくてすむのと、ある程度の強度が得られるのでたまたま目に止まった上記の 商品を用いました。 あとはこの円盤の上に上記のフェライトリング磁石を接着してできあがり。イ ンテリアフェルトの場合は粘着剤がついているので好都合です。製作時間は15 分程度。軸木の先端はあらかじめ鉛筆削りなどで削って細くしておくと回しやす いようです。 このコマを上記の大型フェライトリング磁石の上に浮遊させます。完全自作の U−CASです。U−CASのセットにはコマを持ち上げるためのアクリル板が 付属してきますが、この板の代わりに3.5インチのフロッピーディスクのプラス チックケースを使います。コマがベースの磁石に近すぎると力が強すぎて暴れる ので若干距離をとるのにあのケースの厚みがちょうどいいのです。大型磁石の上 に置いたケースの上でコマを回し、持ち上げていくと、今まで暴れていたのがう そのように、すっと安定する点があります。浮遊点はそのすぐ上部にあります。 コマの質量は一番重要なパラメータです。今回の実験では浮遊時のコマの質量 は15.6gでした。もちろん磁石の組み合わせによって変わります。
| コマの材料 | 規格・型番 | 価格 |
| フェライトリング磁石(外径25.0mm、 内径12.8mm、厚さ7.0mm、質量12.2g) |
ハンズ商品番号 MF-21 | 2個組\280 |
| 銅製たいこ鋲(頭が丸い畳鋲のようなもの、 長さ13mm、頭部径10.6mm) |
ハンズ商品番号 4-061-00113 | 23本入り\130 |
| 木の丸棒 | 90cm | \80 |
| インテリアフェルト(直径28mm、椅子や テーブルの足に貼って床を保護するパッチ) |
北川工業 IF-28 | 8個入り\380 |
| アクリル円盤(直径25mm、厚さ2mmに 加工されたアクリル円盤) |
ハンズ商品番号 13210CR | 5枚入り\180 |
→参考になる元祖U−CASの基礎データはここ。
《U−CASの力学》
U−CASの浮上の原理は言うまでもなく重力と磁気力のつりあいなのですが、 浮かんだ状態が安定であるためには、そこから下に変位すると磁気力が増し、上 に変位すると磁気力が減少して、常につりあいの点に向かって復元力が働かなけ ればなりません。左右に変位した場合も同様です。これらの条件を満たすために、 台の周辺の磁場は前掲の図のような形をしている必要があります。ことに中央上 部での磁力線のくびれが重要です。 もう一つ、なぜ浮く方がコマでなければならないかですが、コマは上がS極で すから逆立ちして台に貼りついてしまうのが一番安定です。この上下反転が起こ らないように、ジャイロ効果で軸方向を保っているわけです。この回転はぜひと も必要で、回転が鈍るとコマは不安定になり逆さに墜落します。
 空中浮遊する全自作のY−CAS
空中浮遊する全自作のY−CAS
《新たなナゾ:コマはなぜ落ちるか》
床との摩擦がないのだから、コマの運動を阻害する要素は空気抵抗ぐらいだと 考えるのは自然です。それさえもなければコマは永久にとは言わないまでも、極 めて長時間滞空するのではないかと・・・私もこれを期待して、実際にやってみ たのです。浮かせる技術を習得して最初に試みた実験です。 用いた道具は真空デシケーターと真空ポンプです。真空デシケーター内にU− CASの台をセットし、普通に空気のある状態で浮くように調節します。うまく 浮かせた時の滞空時間は、空気中では2分ぐらいです。安定して浮いたのを見定 めて、風防としてビーカーをかぶせ、急いでデシケーターの蓋をし、真空ポンプ で排気します。デシケーター内の気圧は、かなり急速に下がり、数十秒で有意な 真空度に達します。この時点でコマはまだ浮いています。見たところ空気中と同 じようにふらつきながら・・・ 空気抵抗は、空気の密度に比例するものなら軽く百分の一以下を達成している はずです。しかし、滞空時間が百倍も伸びるかと期待して見守る目前で、コマは あえなく7〜8分で墜落してしまうのでした。せいぜい数倍にしか伸びないので す。真空中のU−CASはなぜ落ちるか、最後に大きな謎が残りました。
《謝辞》
以上は、本年1月のNIFTY-Serve・FKYOIKUへの私の書き込みと、横浜物理サー クル通信への投稿をリライトし再構成したものです。同所での議論を深めてくだ さり、貴重な示唆をいただいた、理科の部屋の世話人の楠田さんをはじめ、玄武 さん、薬師さん、桑原さん、VECTORさん、梅さん他の皆さん、そして横浜物理サ ークルの皆さんにこの場を借りて御礼を申し上げます。