「日本物理教育学会，物理教育Vol,47,No.2,1999より」

　 フロッピーケース型加速度計を利用した等速円運動の実験

　　　　　　　川村　康文　　京都教育大学附属高校　　〒612-0037　京都市伏見区深草関屋敷町

【抄録】高校物理Ⅱの等速円運動の学習において，現在多くの教科書に取り上げられている生徒実験は「おもりに糸を取り付け，このおもりを等速円運動させる」というものである。しかしこの実験は，実験データの精度の面からと，実際におもりが行う運動が円錐振子となることから，高校生達のあいだではよくない実験として指摘する声もあった。今回は，著者が以前に開発したフロッピーケース型加速度計を利用して「等速円運動」における実験教材の改善を試みた。本実験では，従前からの方法に比較して精度を高めることができかつ，実際にフロッピーケース型加速度計は等速円運動を行うので，前述した問題点を改善することができた。

　　　　　　　１．問題と目的

　高校物理Ⅱの等速円運動の学習における実験では，次に示すような実験が多くの教科書で取り上げられ，いくつかの理科教材会社からは「等速円運動実験セット」として販売されている。中空の筒状のガラス棒を用意し，この棒の中に糸を通す。この糸の両端に種々の質量のおもりを１個ずつ取り付ける。生徒は，ガラス棒を持って，片方のおもりを円運動させる（このおもりを以降「おもり１」という）。円運動しているおもりに作用する遠心力とガラス棒を介して他端に取り付けられているおもり（このおもりを以降「おもり２」という）に作用する重力がつりあうと，円運動している方の「おもり１」は安定した円運動を行うようになる。このときの回転半径ｒ，周回している「おもり１」の質量ｍ，他端に取り付けた「おもり２」の質量Ｍ，回転周期Ｔを測定する。両端に取り付けたおもりの質量や，回転半径を種々に変化させて周期測定を行う。「おもり２」に作用する重力は，「おもり２」の質量をＭとするとＭgとなる。この重力Ｍgは，「おもり２」と糸との結び目で，糸の張力とつりあう。さらに糸を通して，「おもり１」と糸との結び目で，糸の張力は「おもり１」に作用する遠心力Ｆとつりあう。

　整理すると，次のように解釈することになる。非慣性系の立場で観察する場合で説明すると，「おもり１」には遠心力Ｆが作用するが，この力は糸を介して張力とつりあう。この張力は「おもり２」に作用する重力Ｍgによるため，遠心力Ｆの値はＭgと同じ値になる。一方，慣性系の立場で観察する場合で説明すると，「おもり１」が等速円運動をするために必要な向心力Ｆは，糸を介して張力によって与えられるが，この張力は重力Ｍgによるため，向心力Ｆの値はＭgと同じ値になる。

　角速度ωは，ω＝２π／Ｔの関係式によって与えられる。以上の実験操作を経て，Ｆ＝ｍｒω^２という関係式が生徒実験によって検証される。

　具体的な授業展開としては，授業時数の関係などの理由によって次のように行われることが多い。講義形式の授業によって，Ｆ＝ｍｒω^２を公式として先に与えてから，回転半径ｒと「おもり１」の質量ｍと「おもり２」の質量Ｍの値のうちのいくつかを固定して周期測定を行い，この関係式に代入させ，ほぼこの式通りになっていることを検証させる。

　この実験は多くの現行の高校物理Ⅱの教科書に取り上げられている一般的なものではあるが，以前から高校生達にとっては評判のよい実験ではなかった。その理由の１つは，実験データの精度がよくないことであった。一般に，10％～20％程度の誤差がでる傾向があった。誤差の原因として，おもりが周回運動を行う際の空気抵抗の問題やガラス棒と糸との間の摩擦力の問題が高校生から指摘された。さらに，周回している方のおもりの運動は，実際には等速円運動ではなく円錐振子となる。確かに，どの教科書にも，周回するおもりの運動が円錐振子となっても理論的には問題がないと，数式と図解を用いて説明がなされている。大部分の生徒はその説明に満足して，「きっとそれでいいんだ」と納得するが，一部の生徒には「完全な等速円運動（おもりが，ガラス棒の先端を含む水平面内で円運動）している場合と，円錐振子になっている場合では，ガラス棒の先端と糸との間の摩擦力等が変化し，教科書でなされているような理論的説明だけでは納得できない」等の意見がみられた。

　実験データの精度に関する問題では，「同じ回転半径で同じ質量のおもりである」等の条件が一定であっても，回転周期はガラス棒を持っている手のスナップの感覚等である程度幅を持たせることができるという問題点の指摘が生徒の側からなされることが多い。つまり，手加減一つで回転周期の値をある程度の範囲なら自由に変えることができるという意見である。著者自身や多くの教育実習生（何年にもわたり，何名もの教育実習生に行ってもらった）が行った場合でも，可能な限り実験方法に忠実に実験計測を行ってもデータがかなりの範囲で振れたので，高校生に行わせる実験としては，高い精度で行える実験ではなかった。山口・坂田・唐木は，「等速円運動の受容状況と生徒実験の工夫」(1998)において，この実験について「PSSC物理の紹介以来普及したこの実験はなかなかうまい一致を見せず，生徒には不満気であった」としている^１）。

　このような状況のもと，高校生にとって理解しやすい等速円運動の実験教材を開発することが必要となった。そこで今回は，フロッピーケース型加速度計^{２）３）４）}を用いての生徒実験の開発を考えた。また，今回提案する生徒実験においては，等速円運動の関係式Ｆ＝ｍｒω^２を与えてから，実験によって検証するのではなく，高校生が自ら関係式を発見するような授業展開を試行し，その文脈に沿ってデータの整理を行った。

　　　　　　　　 ２．方　法

　大型の水槽を大型の回転台の上に設置して回転させると，水槽内の水面が放物面となることはよく知られていて，各地の科学館の館内展示でみることができる。フロッピーケース型加速度計では，加速度計を手に持って身体を中心軸として円運動させると，加速度が大きな値をとる場合には水面は放物面となるが，加速度の大きさが比較的小さいあいだはほぼ平面になると近似できる。そこで，フロッピーケース型加速度計内の水面がほぼ平面であると近似できる範囲を利用して，「フロッピーケース型加速度計を用いた等速円運動実験器(図1)」を製作した。

　　図１．フロッピーケース型加速度計を用いた等速円運動実験器

　本実験器は，次のような構造になっている。フロッピーケースがぴたりとはさまるような溝がついたカーテンレールを用意する。このカーテンレールの中心を原点として，一方には中心から25cm,35cm,45cmの目盛りを入れ，他方には中心から30cm,40cm,50cmの目盛りを入れる。フロッピーケースの中心をこの目盛りに合わせて，左右に３枚づつ合計６枚のフロッピーケース型加速度計をカーテンレールの溝にはめて取り付ける。カーテンレールの中心に扇風機のモータの軸を取り付ける。扇風機のモータには，100V交流電圧をスライダックを利用して減圧し，30V～50V程度の範囲の電圧をかける。スライダックのアウトプットを一定電圧に固定してモータを定速回転させ，それぞれ６枚のフロッピーケース型加速度計を等速円運動させた。こうすることにより，等速円運動における回転周期Ｔを一定に固定することができる。

　固定された回転周期Ｔを測定し，そのときのフロッピーケース型加速度計内の水面の傾きをビデオカメラで撮影する。この映像をコンピュータのＭＰＥＧソフトを利用して動画としてコンピュータに取り込む。コマ送りで確認しながら，フロッピーケース型加速度計がビデオカメラの正面にきた瞬間をキャプチャーする。キャプチャーしたこの映像をプリンタで出力する（図２）。出力された図から，フロッピーケース型加速度計の水面の傾きθを分度器を用いてよむ。

　図２．等速円運動中のフロッピーケース型加速度計

　よみとった角度θを用いて，それぞれの距離での加速度の値ａを，

ａ＝gtanθ

によって求める。求めた値を表１に示す。

　ここからは，実際の授業展開に沿って，データ処理を行う。表１のように加速度ａ，周期Ｔ，回転半径ｒの３変数が得られた場合，高校生がこれをグラフ化するには３変数を同時に３次元のグラフに描画するよりも，どれか１変数を固定して，残りの２変数についてグラフ化する方が行いやすいと考えられる。そこで例えば，周期Ｔを図３に示すように固定して，加速度ａと回転半径rとの関係をグラフ化する作業をさせる（図３）。また，得られたグラフより，加速度ａと回転半径ｒとの関係式を求めさせる。

　得られた関数式は，ほぼ原点を通る１次式と考えられるので，それぞれの周期Ｔにおけるａ－ｒグラフの勾配a/rをよみとらせる（表２）。

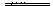
　得られた勾配a/rと周期Ｔの関係をグラフ化させる（図４）。

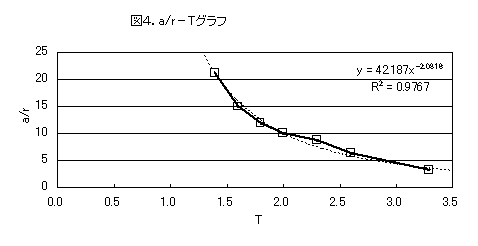
　図４で得られたグラフ（図４では，表計算ソフトにより，当てはめられた関数式が記述されているが，生徒の実際の作業では，グラフ用紙に表２より得られた７点のデータがプロットされているのみである）より，a/rとＴとの間にどのような関係があるかを生徒達に考えさせる。

　この場合，生徒の多くはa/rとＴとは反比例の関係であると予想するので，一度は，a/r－1/Tグラフを描かせてみる。a/rとＴが反比例の関係の場合，a/r－1/Tグラフが原点を通る一次関数になることについては既習事項であるので（例えば，物理ⅠＢでの運動の第２法則を生徒実験として行い，データ処理をさせる過程で，Ｆ＝ｍａにおけるｍとａの関係は反比例なので，ａ－1/mグラフは正比例となることを経験しているなど），a/r－1/Tグラフが原点を通る一次関数にならないことから，「a/rとＴとは反比例の関係である」という誤った考えは生徒の実体験により棄却される。そこで，あらためてa/rとＴとの間にどのような関係があるかを生徒達に考えさせる。少し時間はかかるが，やがて「a/rとＴ^２が反比例しているのではないか」とか「a/rとＴ^ｎが反比例しているのではないか」という考えが提案される。後者が先に提案された場合には，「簡単な数値から調べてみましょう」と教師側からもちかければよい。いずれにせよ，生徒自身の手によって，a/r－1/T^2グラフが作成される。またそのとき，a/rと1/T^2の間の関係式も求めさせる。表計算ソフトを用いて，著者が作成したグラフは図５のようになった。

　　　　　　　　　３．結　果

　図５より，今回の実験データ処理においては，

a/r－1/T^2グラフの勾配Ｋは，Ｋ＝39.99であることが導かれる。この結果，原点からのずれを誤差として，

ａ＝39.99*(1/T^2)*ｒ

と関係式を求めることができた。ところで，ω＝２π/Ｔなので，

ａ＝1.01rω^２

となる。これは，１％の誤差で向心加速度を求めることができたことを意味する。

　この後の授業展開は，多くの教科書に記述されているように，向心力Ｆは，運動の第２法則により，

Ｆ＝ｍａ＝ｍrω^２

として求められる。今回の実験により得られた向心力Ｆは，

　　　　Ｆ＝1.01ｍrω^２

となり，１％の誤差で求められたことになる。

　　　　　　　　　４．考　察

　一般に，生徒実験を行う場合，力学分野では10％～20％程度の誤差がでることが，おうおうにして起こりうる。教師が実験を行ったからといって誤差を０％にすることも現実には不可能である。このような状況をふまえて，今回の実験結果をみつめなおした場合，本論文で紹介したような簡単な実験装置で，最終の実験式の誤差が１％で求まった。このことは，学習効果を高めることができる生徒実験の教材としての可能性を示唆しているといえよう。

　生徒達にできるかぎり実際に実験器を操作させながら実験を体験させることは大切であると考えるが，本実験器具の製作は比較的簡単なので，実際に生徒実験を行う場合に，各実験班に１台ずつ実験器を与えて，各実験班ごとに実験をさせることが可能である。また，本実験器具の製作は高校生でも十分可能であるので，現行の物理Ⅱの課題研究のテーマとして，実験器の製作場面から，高校生に研究課題として与えられるのではないかと考えられる。

　生徒はよく，実験結果の精度の高さに感動し，興味・関心を示すが，このように簡単な実験器によって精度高く実験結果が求められる実験は，生徒にとっても「やりがい」が感じられ，生徒に受け入れられる実験の一つになるのではと考える。

引用文献

1)山口浩人・坂田正司・唐木宏「等速円運動の受容状況と生徒実験の工夫」物理教育Vol.46, No.2, 1998, pp.61-64

2)川村康文「遠心力再考」京都理化学協会会誌，1986年度版，pp.3-40

3)川村康文「フロッピーケース型加速度計」近畿の物理教育第３号，1997，pp.25-28

4)川村康文「実験で知ろう！おもしろ科学(31)加速度をを計ってみよう」Ｌ５(1998年10月号),日本宇宙少年団，1998,p12

　　付　記

　本研究は，京都府立西城陽高校の山口道明先生に，著者が開発したフロッピーケース型加速度計を回転円盤上に取り付けて等速円運動を行わさせた場合のデジタル写真映像を平成９年12月に見せていただいたのをきっかけに始まった。著者はそれ以前から，本実験器のアイデアをあたためていたが，実際に製作し，試行実験してみようという原動力を与えて頂いた。深く感謝申し上げます。

　また本実験器の原型は，電動式ではなく，自転車の車輪を用いて，それに本実験器と同じ「カーテンレールに６枚のフロッピーケース型加速度計」を取り付けた手動式のものであった。その実験器は，平成10年度の教育実習生が３月から４月にかけて製作し，本年度５月の教育実習生による「等速円運動の授業」で実際に用いられ，本報の「３．結果」に示したような授業展開が行われた。しかしこの手動式では減速が激しく，データの精度も高くはなかったので，今回の電動式実験器に改良された。