　　　　　　　　　　　　　　　　　　　　　　　　　　　２０１４年７月１２日（土）

　　　　　　　　　　　　　　　　　　 ○×ゲームを考えよう　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　京都府立桃山高等学校　中村　啓介　先生　　　　　　　　　　　　　　　　　　　

推薦して頂いた「布武」で，お食事を済ませました！ハーブ奏者のミニコンサートを聞きながら，松花堂弁当を味わうという変わった
シチュエーションでしたが，美味しかったぁ～。次回も是非昼食場所のお薦めを楽しみにしています。


お馴染みの○×三目並べゲーム。先手○・後手×を交互に１マスずつ置く。さて，先手が必ず勝か？後手が絶対勝てる方法はあるのか？　(「決着つきません」と多数が挙手)	ルール改正：盤を広げて，写真の左上図の4マスの図形が出来たら勝ち！

【テーマ】普通は先手が有利だけれど，後手が粘れば勝負がつかない形があるはずである。それを見つけよう！
　　　　　　　　　　　　　　　　　　　　　　　　　　

１マスを「セル」と名付けて，セルでできる図形は，「裏返し」や「回転」をしても同じ図形であると考えることにします。

【１セル】

　は先手が打った瞬間勝ち！　【２セル】

　は先手→後手→先手となり、必ず何処かで２つ繋がるから先手の勝ち

【３セル】

　も先手が先に必ず作れる。

　も先手が必ず先に作れる。他に３セルでできる図形はあるでしょうか？


４セルのときは，何通りあるか。考えてみようよ。　　　　　答え　5通り	４セルで勝負が付かない図形がどれなのかを見つけるために対戦しよう！！　　（仲むつまじく議論が始まりました）

５セルの場合も，６セルの場合についても、

①「異なる形が全部で何通りできるのか」

②「対戦したときに，先手も後手も絶対に作れない図形は，①の中のどの図形なのか」

を考えることにしました。

４セルの場合

　この図形のみです。　　５セルの場合は、①は１２種類，②の図形は①の図形のうち９つあります。
　　　　　　　　　　　　　　　　　　　　　　６セルの場合は，①は３４種類，②の図形は①の図形のうち３３個は分かっているのですが，

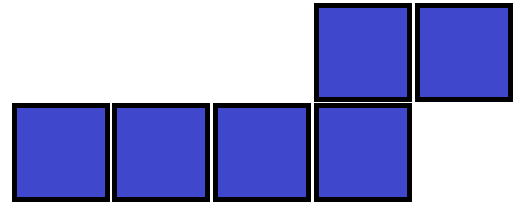　は唯一未解決らしい。　　　　　　　へぇ～、ほぉぅ～、と感嘆の声がチラホラ

　　　　　　　　　　　　　※ここで裏話ですけれど，
　　　　　　　　　　　　　　

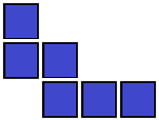　が抜けていたらしい。６セル場合は，全部で３５種類でした。皆さんは、ちゃんと数えた？

　●先手であろうが後手であろうが，絶対に勝とうとするのではなくて、絶対に負けないように工夫すれば良い。
　「勝負の決着」が付かないように戦略を練るのも1つの生き方です。　　　　　　　　　　　　　　　　　　　　　　　　　　　
　【畳敷き戦略】　

　のように２セルで１枚の畳。後手は先手が色を塗ったもう一マスを必ず塗る作戦。


ルール変更をしてオリジナル三目並べを作りましょう！受講生の独特な発想と柔軟なアイデアは、先生でも太刀打ちできません。こんなルールを良く思いつきますねぇ

色々な例を紹介してもらい，どんどん可能性が広がっていくことが分かりました。式の計算ばかりをしているのだけが、算数・数学では
ありません。
しっかりした戦略を立てて考えていく【論理思考力】も算数・数学を学ぶ価値なんです。

　　　　

　　　　　夏の自由研究に如何ですか？　　　　　

参考・引用文献：
１）2011年組合せゲーム・パズルミニプロジェクト
２）本田耕一，「一般化三目並べの拡張における勝敗判定に関する研究」，東北大学大学院情報科学研究科，２０１１