２０１４年７月２７日（日） 　　　　　　　　　　　　　　　　　ちょっと階段のぼってみない？　　　　　　　　　　　 　　　　　 　　　　　　　　　　　　　　　　　　　　　　　岐阜県立飛騨高山高等学校　荒川　公則　先生

　【配布資料】　→　　　　　　このときの模様は，7月28日付岐阜新聞県内版に掲載されました。　→　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

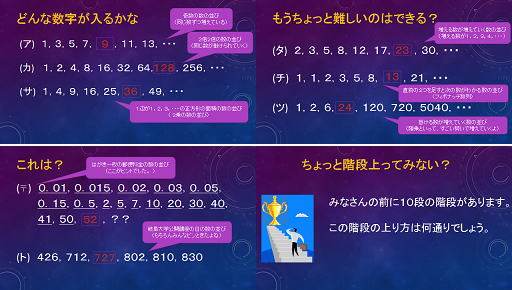
本日の講師は荒川先生（飛騨高山高等学校）です。	空いた所に入る数字を見つける頭の体操と数列について簡単にレクチャー。ア〜順番に問題記号が付いているはずなのに．．．．。それがヒントになっています。	会場の様子

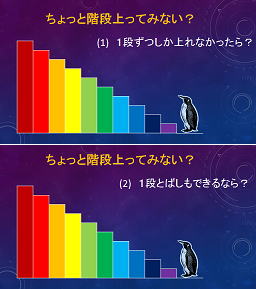
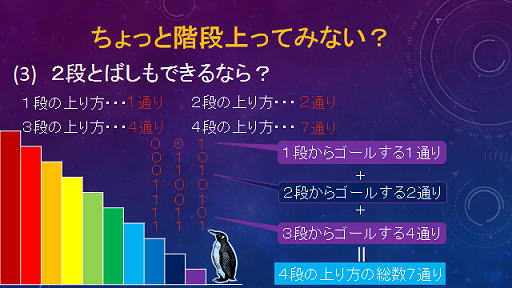
10段の階段を1段ずつしか上がれない場合と１段飛ばしも可能な場合と何通りあるか数えてみよう。	受講生が自分の考えを説明しようとしますが、なかなか上手く説明できないぞ	そこで法則性を見つけるために２つのヒントが与えられました。(1)階段が全部で1段しかなかったとき，２段しかなかったとき，３段しかなかったときで考える。(2)ゴール直前のときに何段目にいたかも序でに考える。とすると，４段目がゴールのときは、（２段までの２通り）＋（３段までの３通り）＝５通りあることに気付く。つまり５段目をゴールとすると、（３段までの３通り）＋（４段までの５通り）。少し分かってきた？？

ということで，順々に計算していくと１０段目で，　８９通り　あります！！

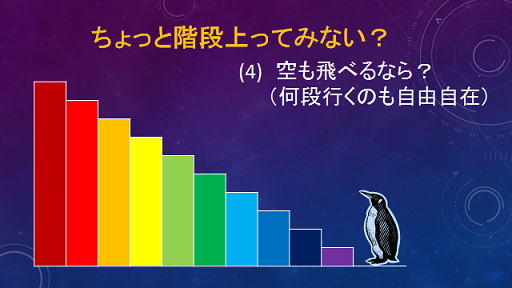ちょっと勢いをつけて２段とばしまでできるならば、どうなるか考えてみました。	実は1段とばしの問題も、２段とばしの問題も、この問題の前ふりでした。さぁ、何段とばしでも可能ならばどれだけの方法があるでしょうか？難しいぞぉ

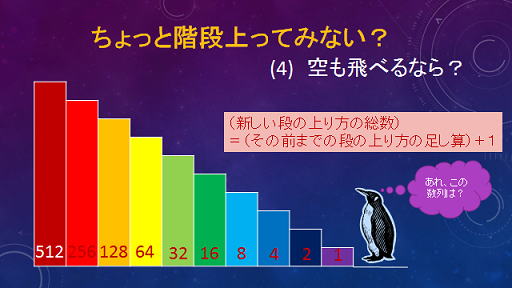
もぉ〜。私達数え疲れちゃった。おやつが欲しいわぁ〜	たとえば，５段目の１６通りという数字は、１＋２＋４＋８に１を加えています。	数字の様子が複雑になってきた

ここで、○○進法について簡単な講釈をしますね！ １０の位，１００の位，１０００の位という数字の世界は良く慣れ親しんでいる世界です。例えば，２０１４は， ２×１０００＋０×１００＋１×１０＋４×１と表して、それぞれ位の頭数字を取って，２０１４としています。 ここで，１０００＝１０×１０×１０のことで１０を３回掛けるので、１０３（１０の３乗）と表すことがあります。 １０００００＝１０５，１００＝１０２，１０＝１０１，１＝１００（１０を１回も掛けませんという意味で考えましょう） と表せます。 つまり，２０１４(10)＝２×１０３＋０×１０２＋１×１０１＋４×１００と表現できるので、これを １０進法で表す数としましょう。 １０進法の数は、また１０の一固まりになろうとすると、次の位に上がることは良く知っていますよね？ それでは，２進法はどのように考えれば良いでしょうか？ ２の一固まりになろうとすると，次の位に上がるのです。つまり，０，１，１０，１１，１００，１０１，１１０，１１１，・・ と数字が順々変わっていきます。１０進法で表した数字と同じように２進法でも考えると， 例えば，１０１１００１(2)＝１×２６＋０×２５＋１×２４＋１×２３＋０×２２＋０×２１＋１×２０ と表せて、それぞれの頭数字を取って，１０１１００１としているのです。 ２進法と１０進法との対応関係は，０(2)＝０(10)，１(2)＝１(10)，１０(2)＝２(10)，１１(2)＝３(10)，１００(2)＝４(10)， １０１(2)＝５(10)，・・・・となります。 そうすると，１０１１００１(2)＝１×２６＋０×２５＋１×２４＋１×２３＋０×２２＋０×２１＋１×２０ 　　　　　　　　　　　　　　　＝６４＋１６＋８＋１＝８９(10) となるのです。

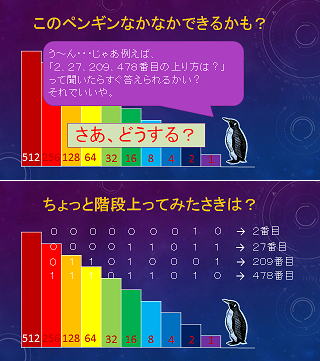
それぞれ適当な昇り方の番号を決めると、図のような０と１の暗号になってしまいました。これこそが２進法になります。

　不思議な数字の世界．．