２０１４年８月３０日（土） 　　　　　　　　　　　　　　　いろんな形の面積をもとめてみよう　　　　　 　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　立命館宇治中学校・高等学校　稲葉　芳成　先生

今日の講師は稲葉先生です。とりあえず図形の面積の復習 をしよう	満員御礼。さっそくですが，15cm ×20cmにパンチングボードを充て	ただひたすら「規則正しく」点を打つべし！ダダダ・・

規則正しく並んだ点は全部で710 個にしよう。個数が2倍になれば 面積も2倍になるはずだ。	面積300cm2で710個のドットを基準にしましょう。台形も同様 に，パンチングボードで，ただひたすら点を打つべし！ ダダダ・・・	えっとぉ〜。１８０個打てたから，台形の面積は大凡 ○○○cm2だよね。（皆さんも一緒に考えてください）

半径５ｃｍの円も，ただひたすら点を打つべし！　ダダダダ・・・	188個打てたので，円の面積は79.4cm2。実際に計 算した78.5cm2とほとんど変わらないんだぁ!!	それでは岐阜県の地図があるから，面積を計算しましょう。ダ ダダダダダダ・・・さすがに疲れてきたかぁ〜

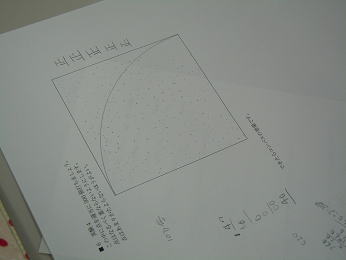252個打てたので面積は求めら れるけど、縮尺があるぞ。実際 km2で出してごらん。	岐阜県の面積は、地図帳にも書いてあるし，岐阜県が全国８ 位の広さも良く知っていました。 次はパンチングボードは使わ ずに10cm×10cmの正方形上に均等に点を300個打ってみます。	コンパスで1/4円を描いて，その中に含まれる点と外にある点 の個数を考えて，面積を計算します。

	ドットを打っていくことは、本当にどっと疲れたことで しょう。 こんなときコンピュータを使用すると便利なんですよ。 　　　　　　　　　　当日の配布資料 　　　　　　　　　　当日のスライド
円の面積が求められ、π：円周率の大凡の値が導かれることになるのです。	モンテカルロ法について調べて，挑戦してみよう。

本日は、講習の最後の授業。夏休みの自由研究の素材探し？宿題？を目指した人が多かったから、参加人数が増えたのかなぁ？？？
また，次年度もできるように，講師陣に感謝の拍手を送って下さい。

※中日新聞「Ｄｏまんなか」（9月20付）掲載記事

では，また今度どこかで、ね。　　　　　　ごきげんよう、さようなら

■ 概要
　小学校の算数科では様々な正方形や長方形をはじめとしてさまざまな図形の面積の求め方を学習します。そのような図形の面積を求めるには辺の長さや図形の高さを測ったりすることが必要です。今回の第６回講座では、ちょっと形がゆがんだ図形や曲線で囲まれた図形の面積を求めることにチャレンジします。そのような図形では曲線の正確な長さなどを求めることができないために、定規ではなくある簡単なモノを利用します。その簡単なモノを使えばその図形のおよその面積を求めることができます。さてそのあるモノとは？そしてその使い方とは・・・？

■　講座における今次内容の流れと算数・数学的意味付け
今回とりあげるのは面積比を用いた様々な平面図形の求積です。算数科・数学科では通例では長方形の面積などを具体的に求めたり面積公式として扱えるようにします。学年を進につれて扱う図形もおおくなったり曲面である円の面積を求めることも学びます。
しかし実際の生活場面においては典型的によく知られた平面図形よりも複雑であることが多く、いくつかのよく知られた図形に分けて考えることでも難しいものも多くあります。また円でない曲線で囲まれる領域の面積を求めることも必要となってきます。これまでそのような図形や領域の面積を求めるには、基本となる単位図形、普通はひとつの面積簡単にわかる細かい正方形や長方形に分割してその数を数えることで面積を求める方法が紹介されることが多いと思います。
今回はそうした求め方とは異なる方法をひとつ紹介します。ある基本的な図形を基にして、その図形の面積を既知としたときに、それとの比をとることで求めたい図形の面積を知るという視点は同じですが、実際に求める過程は少し異なります。そして今回は簡単な道具を用いることで小学生などの学齢の低い児童にも興味を持たせながら、実際に作業的に手を動かすことで飽きさせない方法を模索します。
これがうまくできればそれにつながる方法もあわせて紹介します。それは一般的にもよく知られた方法でもあります。