２０１５年５月３０日（土）  　　よく回るコマを作ってみよう！　 　　　  　　　　　　　　　　　　　　　　小川　陽介 先生（岐阜県立大垣東高等学校）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　講座で使用する計算シート，　図形シート
目的：平面図形の重心の求め方を考え，岐阜県の重心を求める。

重心：重心とは物体の各部分に働く重力の合力が作用されると考えられている点。　　　　　　　　　　　　　　　　
つまり、図形を指1本で支えられる点である。ただし、その図形が均一な物質でできていると仮定する。　　　　　　　　　　　　　　　　　　　　　　　

方法：適当な多角形を用意し、多角形の重心について求め方を考え、まとめる(理論上の重心)。
図形を厚紙で模り、実測し、理論上の重心と実際の重心とを比較し、一致することを確かめる。
多角形の重心の求め方を一般化し、その求め方を応用して、岐阜県の重心を求める。

お薦め本：　『暗号解読―ロゼッタストーンから量子暗号まで』　サイモン シン (著), Simon Singh (原著), 青木 薫 (翻訳) 　新潮社

均質な重さの三角形の板の重心の見つけ方を聞きます。 なんと！パワーポイントのアニメーションが動かなかった のです。	でも、何も無かったように受講生には分かりやすく説明して もらいました。さぁ、図形シートの三角形の重心を求めて、 切り抜きをします。	図形の面積の大きさを「重さ」と考えて，重心を計算して そこに穴を開けます。爪楊枝を差し込み。回してみます。 ほら！キレイに回転しました。
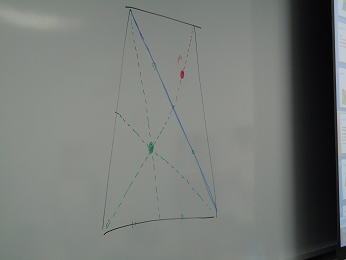
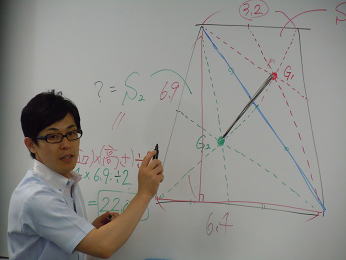
四角形の場合は，２つの三角形に分けてそれぞれの 重心を同じように求めます。２つの重心を結んだ線分の 何処かに四角形の重心があります。それは２つの三角形 の面積の値の「逆比」となる点を線分上に決めれば良いのです。	では図形シートの四角形の重心を「計算」して、コマを作ります。 本当は面積の計算がそこそこ大変なのに、電卓を忘れた受 講生がそこそこおりました。でも、一生懸命計算し、．．．．． ほら！ほら！キレイに回転しました。	最後に、岐阜県のシートをコマにしてみましょう。 でもあまりに 複雑な形です。そこで入り込んだ輪郭を直線で省略して、簡単 な多角形にします。幾つかの三角形の重心を求めて、さぁ 計算をしましょう。

四角形のコマ作りの時から、手元に電卓のない参加者のことを 本当に心配されていた講師の先生。ハラハラしていましたが、 文句も言わないで、一生懸命計算するのですね！ ほら！ほら！ほら！キレイに回転しました。

先生の心配を他所に、受講生のたくましさに感心しました。ところで高校の理数科では、これをコンピューターの表計算ソフトを用いて
緻密に計算します。とすれば、岐阜県の重心となる「地名」が見つかるのです。果たして、どこなのでしょうか。　　　　　　　　　　　それは自由研究だね。