２０１５年９月２６日（土） ビーチボールをぺったんこ！？ −球面図形への誘い−    　　　　　　　　　　　　　　　　紀平　武宏 先生（京都市立紫野高等学校）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　この講座で使用したワークシート，　　地球儀シート

　　　お奨め本：　『アートを生み出す七つの数学』　著者：牟田　淳　出版社：オーム社　　　　　　　　　　　　 　　　　　　

直方体と球体をペッタンコにして、平面にする ことができますか？	球体を平面にすることはできないぞ。曲面っ て何？	平面上の「直線」とはを振り返り、その定義を 基にすると、球面上の「直線」ってどんな線に なる？ ボール上に点を2つとって、結んでみましょう。

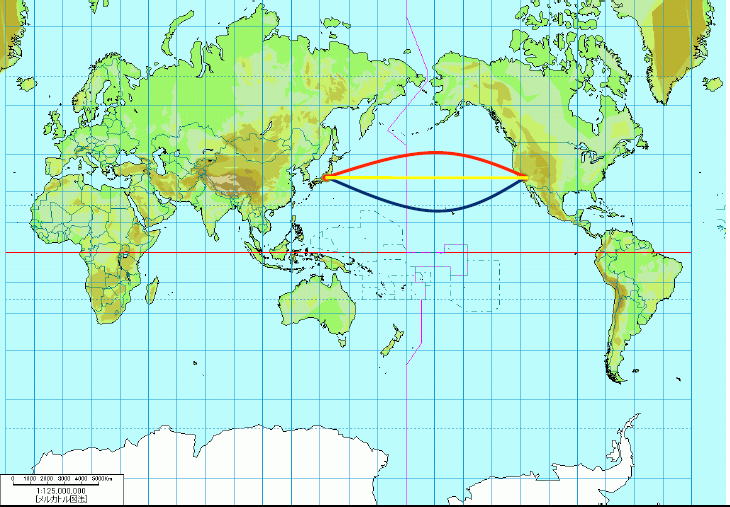
メルカトル図法の世界地図。これを丸めて球体ができますか？東京からロサンゼルスまでの最短経路はどれですか？地球を組み立てて、調べてみよう。	展開図から地球を組み立て 経線と緯線の仕組みを考え ます。	次に10種類の地図（長方形）を配布しました。どうも 岐阜市域の地図のようです。自分達の家や施設が何処 にあるか確認してみましょう。

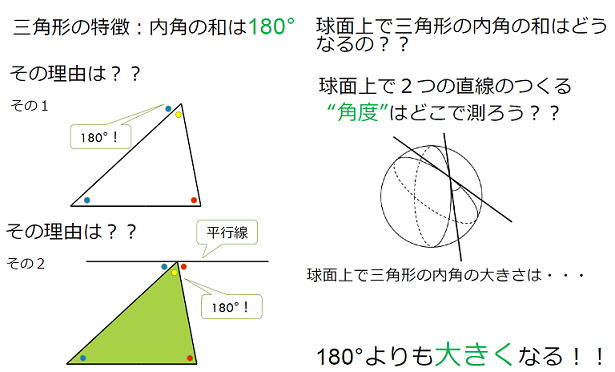
その10枚の地図を合わせて、1枚の大きな地図にしてみまし ょう。ん、ん、1枚1枚は長方形だと思っていたのですが。 少しずつずらさないと1枚の地図になりません。長方形は見た感覚で少しずつ 歪んでいることに気づくことになりました。	平面上の三角形の内角の和は、180゜ですが、どうしてですか？理由を考えてみましょう。経験的なものなのか、分度器で測ったから、平行線における同位角、錯角を使って（演繹的）、........では､球面上の三角形の内角の和はどうなるのでしょうか？

　　　　すごく基本的なことからジワジワと話が進められたので、少し算数に苦手意識のある参加者や小学校５年生にとっては
　　　　心地よかったみたいです。

　　　　　　でも、北の方角に１ｍ進み、西の方角に１ｍ進み，南の方角に１ｍ進んだら、元の位置に戻りました。
　　　　　　はてさて、私は地球のどの位置にいるのでしょうか？（昔良くあったナゾナゾですが、今の子達には通じなかった．．．．）