 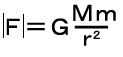 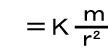 ( G:6.67×10-11 (万有引力定数) |
点Pにある物体を,限りなく無限遠の位置に移動する。 位置エネルギーは, 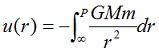 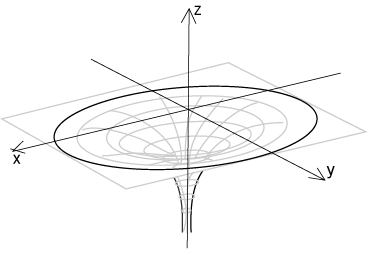 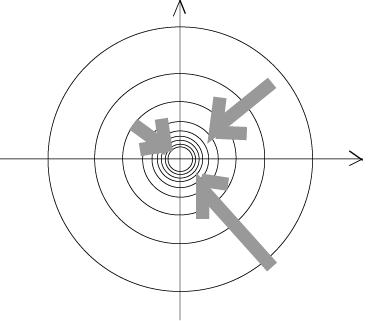 |
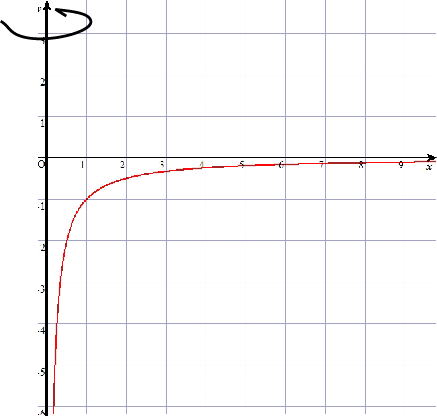 ② 簡単に説明すると,上図のように 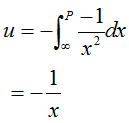 という分数関数のグラフが描けます。 |
| 重力の逆2乗法則(万有引力の法則) | 位置エネルギー | この曲線をy軸の周りに回転すると左上図のような立体ができるということになります。 |
万有引力の位置エネルギー 河崎哲嗣 mathEnetのホームページへ
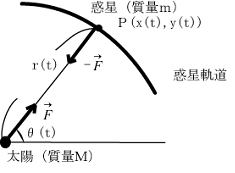
理系分野への進学,科学者を目指す生徒に対する科学教育として,近代科学の礎であるニュートン科学は,重要だと思います。
ニュートン力学といって想定されるのは,万有引力の法則や運動方程式です。ニュートンは,ケプラーの惑星運動法則に関して数学的に証明(プリンキア)を与えたわけです。
では,そんなに大切な科学観であるならば「現在の高校生に対して,ケプラーの惑星法則やニュートン力学が触れられる所は,どの辺りなんだろう?」と探しますと,扱える分野は「微分・積分」でしかも「微分方程式」の分野となります。
この領域は,今のほとんどの高校生にはとても辿り着けない分野になってしまっています。40年前の教科書では,高校生の当然の素養のように扱われていましたし,指導する側もそれなりに準備していたのでしょう。扱われていないから見過ごすというほど,この分野を決して疎かにできるわけではありません。
せめて有用性だけでも生徒に伝えたいと思いばかりが先行したわけです。
どんな風に持って行こうかと,うだうだ悩んでいましたら,
「高校の微分・積分は,力学も目指して,万有引力の法則から惑星の楕円軌道まで扱うべき」
という提言に出会いました。微分方程式は,積分の一種です。
1次関数を無限につないで,その変化の再現をする(微小な要素の集まり)
という概念を,如何にして浸透させるか,ニュートンの科学理論に学んで,自然科学と関連があるケプラーの法則まで証明してしまう経緯を簡潔にする工夫を試みました。
※この内容の詳細は,別途論文にしましたので割愛します。
①さて,軌道を見せるために,面白い教具を考えました(見つけました)
 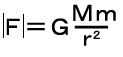 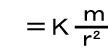 ( G:6.67×10-11 (万有引力定数) |
点Pにある物体を,限りなく無限遠の位置に移動する。 位置エネルギーは, 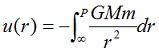   |
 ② 簡単に説明すると,上図のように 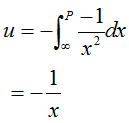 という分数関数のグラフが描けます。 |
| 重力の逆2乗法則(万有引力の法則) | 位置エネルギー | この曲線をy軸の周りに回転すると左上図のような立体ができるということになります。 |
③コンピュータでシミュレーションしたり,映像で楕円軌道を見せることはできます。
しかし,このような回転体の実物があれば焦点付近で加速しているのを,感じ取れるのではと考えました。
④色んな伝を利用して探しましたが,そんなものがあったとしても持ち運びもできないし,
教具屋さんに頼んだら製作費用が,高額になると言います。
半年ほどかけても見当がつかず,諦めかけた頃,なんと
偶然適当な物を見つけました!!!!
| 断面図です。曲線の回転体になっています。 | 中を覗くと穴があり,手で握って振ること もできます。 |
実は,貯金箱になっていて穴には渦を描いて入っていきます。 動画にすれば良いのですが,それは科学館へ行って,実物でも 見てください。 |
コインが落ちていく重力に逆らって,焦点付近で加速して振るように意識するとコインは逆に昇って回転します。焦点から離れて減速し,焦点付近で速度を上げることを身体が理解していくという教具?おもちゃ?です。
曲線をもっと伸ばして大きな皿にすれば良いのですが,それは次の課題。
そういう物は販売されていて取り寄せの場合だと,20万円以上!なんとも良い物は高価ですね。
(買います?勇気のある方は,河崎まで) 京都府数学研究会
了