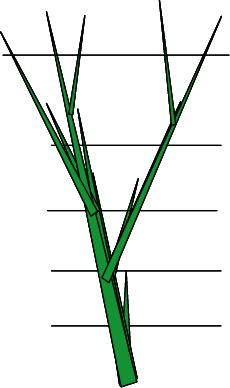
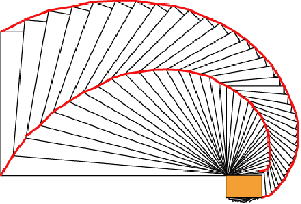
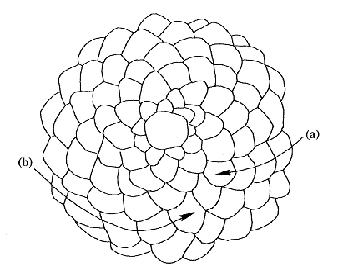
木の生長とフィボナッチ数 松かさ
2004年6月12日(土) 目の感覚を利用しよう 河崎 哲嗣先生 「京都教育大学附属高校」
講演者が小学生の頃、「図画工作の授業で写生(遠近法・グラデーション)は「黄金比」を用いるとうまく表現できる」ということを学んだ回顧録から、
やや早急でしたが、黄金比の紹介(生活につながるフィボナッチ数)から遠近法のトピックスを盛り沢山に掻き集めました。



木の生長とフィボナッチ数 松かさ

葉序(葉のつく順序) 大凡5角形 「じゃがいも」はどちらが上?下? →芽のある方でしかも螺旋。葉も芽も互いに光を遮らないように生きているんだ。
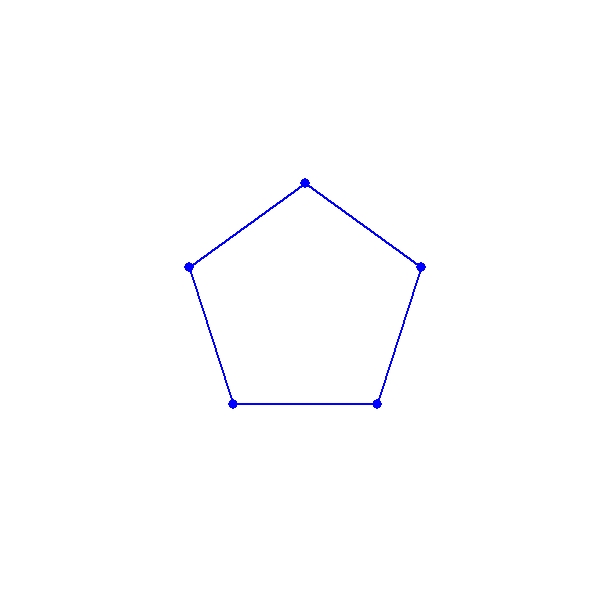
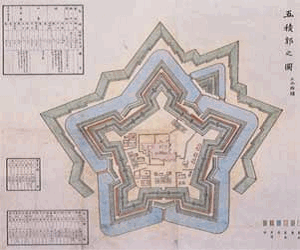

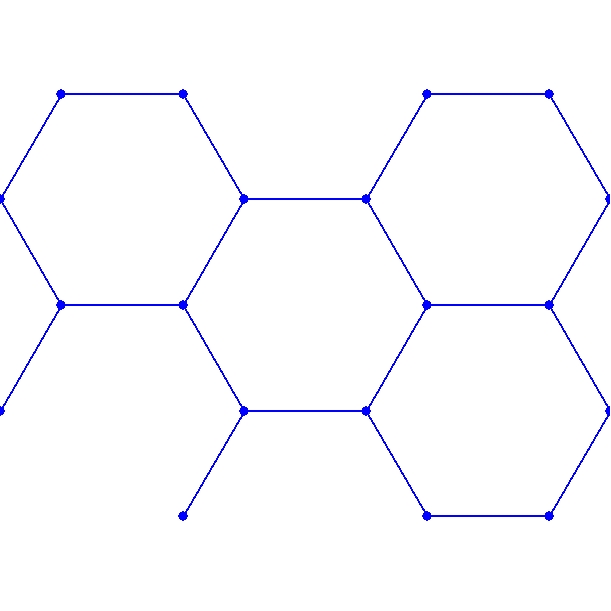
正5角形は、黄金数の宝庫。 平面上での正多角形の「敷き詰め」。物質間で最も安定しているような正6角形。 しかし、立体(生物の生長点のような)にすることはできない。
「フラーレンC60」の紹介→6角形に1つ5角形を混ぜると立体になる。 カーボン・ナノチューブの模型
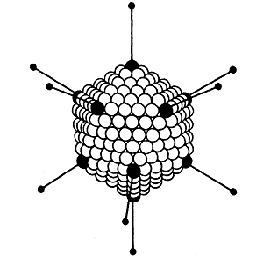
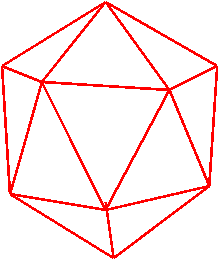
ウィルスの増殖(正20面体)これも黄金比(5角形)らしい。→菱形多面体による空間敷き詰めの局所部分
疑問だったので、右上のようなパズル型立体模型を作りました! 「名刺」・・・(黄金長方形)3枚準備して作り角を竹籤で接着。
ほら!5角形があるでしょ!

正4面体3個を組み合わせたクリスタル型。ここにも黄金長方形がでている。
今回は作業が多くて申し訳なかったなぁ〜。
パズル製作、1等賞(どこかのお母さん)は、パイナップルをあげました。ゲット。(これが一番嬉しかったかな?)
さて、後半戦。
図画工作の授業「写生の遠近法」のコツ(黄金比分割)について当時小学生の講演者に伝授された工夫は、当時良かったことでした。
しかし、本来の原理はどうなのか簡単にレクチャーをして、その後生活の中に介在するトリックアートの紹介と「エイムズの部屋」を作成してみました。

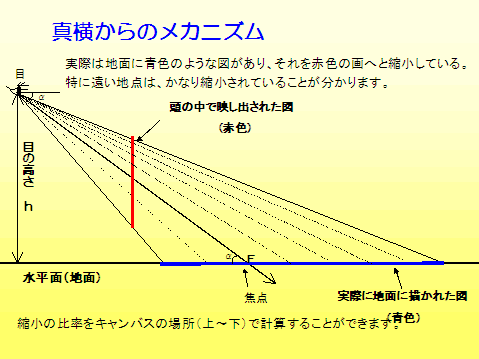
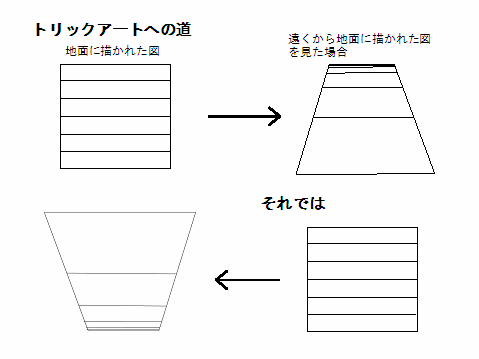
通勤途中の自転車・歩道 射影幾何の実験
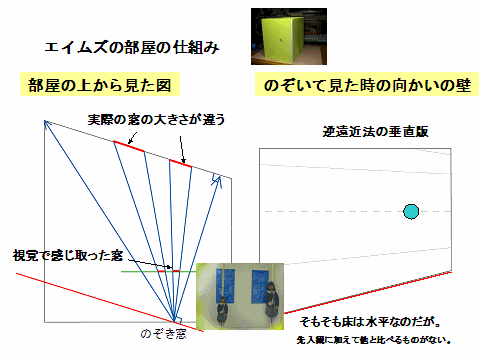
エイムズの部屋(目の錯覚) 最後は、時間延長して作ってくれました。  終わり お疲れ様でした。
終わり お疲れ様でした。