平成１３年度新教科「情報」現職教員等講習会：モデル化とシミュレーション教材例
放射性崩壊のモデル
神奈川県立湘南台高等学校 山本明利
放射性原子核はα線やβ線を出しながら壊変して他の原子核に変わっていきます。壊変は純粋に確率的に起こります。あるひとつの放射性原子核が、次の単位時間に壊変する確率をλで表し崩壊定数と呼ぶことにします。各放射性原子核の壊変は独立事象ですから、ある時刻ｔに残っている放射性原子核の個数をＮとすると、Ｎは単位時間にλＮだけ減ることになりますから、次の式が成り立ちます。
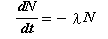
これが崩壊法則です。これを変数分離して積分すると次式を得ます。ただし初期条件、ｔ＝０でＮ＝Ｎ０を用いています。
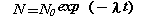・・・（１）
放射性原子核の数は指数関数的に減少していくことになります。ここで、放射性原子核数がはじめの半分に減るまでの時間として半減期Ｔを定義すると
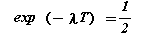
となりますから、崩壊定数λは半減期Tを用いて次のように表すこともできます。
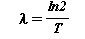
ｌｎは自然対数を表します。これを式（１）に代入して整理すると次式を得ます。
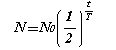
高等学校の物理ＩＢの教科書には、この最後の式が載っているわけですが、導出は一切ありません。高校物理では積分は原則として使わないことになっていますし、まだ数学ＩＩＩは習っていませんから・・・。生徒はなぜこの式が成り立つのかという背景も知らず、指数関数としての性質もよくわからないまま、これを公式として覚え込むという邪道に走ることになります。
そこで、物理の授業では苦肉の策として、たくさんのサイコロを振って、特定の目が出たらとりのぞくとか、多数のナットをばらまいて裏返ったものを除いていくという「モデル実験」により、各回ごとに残ったサイコロやナットの数に同じ傾向が現れることに気付かせ、放射性崩壊が確率過程であることを納得させています。でも、はっきり言ってこの実験は面白くありません。
どうせモデル実験しかできないなら、表計算ソフトの乱数機能を使ってシミュレーションをしてみたらどうでしょう。いちいち数える手間もないし、グラフも同時に描いてくれるのでスマートです。それではさっそくやってみましょう。
ここをクリックしてdecay.xlsを開いてください。（MS-Excelが必要です）
ファイルサイズを小さくするため、はじめは１個の原子核しか登録されていませんので、表内の説明にしたがい、最後の行を下へコピーして５００〜１０００個にして実行してみてください。
ホームページに戻る