「愛知の理科教育1982」と全国の物理教師の有志が名古屋に集結した「電磁気学の集中講義」の記録です。
早速、読んでみましたが、当時の参加メンバーは今は定年を迎えられている方が大半で、高校を初め、様々な立場で活躍されている方々の若かりし頃の激しい討議の様子が伝わってきました。

2014年7月5日の記録の第2ページです
| 貴重な資料 (飯田さん) |
| 飯田さんが昔の資料が何冊か見つかったので、誰かのためになればと配布してくれました。 「愛知の理科教育1982」と全国の物理教師の有志が名古屋に集結した「電磁気学の集中講義」の記録です。 早速、読んでみましたが、当時の参加メンバーは今は定年を迎えられている方が大半で、高校を初め、様々な立場で活躍されている方々の若かりし頃の激しい討議の様子が伝わってきました。 |
 |
| 30年以上前の貴重な資料です。 |
| ローレンツ変換 (飯田さん) |
| M.ボルン「相対性理論」を読んでいたところ、ローレンツ変換の比例定数aを求めるのが非常にややこしかったので、いろいろ考えていたら、簡単な求め方を閃きました。 今、2つの慣性系を考えます。1つは地面、もう一つは等速vで直線を進む列車です。 アインシュタインの相対性理論によると、座標系によらず光速は不変であるので、 x'=ct'(-①),x=ct(-②) 慣性系はどの座標系から見ても等価であるので、どちらから見ても等価になる比例定数aを用いて、 <列車内の座標を地面の座標で> ax'= x - vt (-③) <地面の座標を列車内の座標で> ax = x'- vt'(-④) と表すことができる。 ここで、①②式を③④に代入すると、 |
 |
| エレガントな求め方です。 | |
| act'= ct - vt = ( c - v )t (-③') act = ct'- vt'= ( c + v )t'(-④') となります。 そして、ココがポイント!③'×④’をします。 a2c2 a2 = (c2 - v2)/c2 ∴a=√1-(v/c)2 と求まります。 |
|
| クリップモーター製作の工夫 (児島さん) |
| 飯田さんのクリップモーター改良の記事を見て、児島さんがアイデアを持ってきてくれました。 まず、重心を真ん中に取るための工夫としてナットにコイルを巻くことで、ほぼ正六角形のコイルを作りました。 |  |
| 六角形は重心を特定しやすく、型が入手にしやすいです。 | |
| さらに、電池ケースにネオジウム磁石を付け、電池ケース内部の電池と接触するようにクリップを引っ掛け通電するようにし、そこにコイルをのせました。 慎重にコイルをのせることができれば、かなり安定して回ってくれます。 素晴らしい工夫ですね。 | 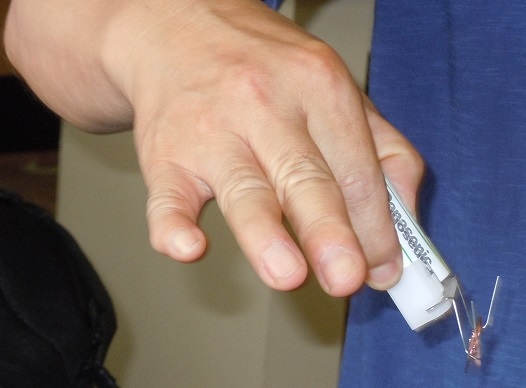 |
| クリップにかけられたコイルが勢いよく回転します。 | |
 |
児島さんはモーターの仕組みを理解させるために、市販のマブチモーターを分解し、モーターの内部をモーターの軸に固定することで、中身の見えるモーターを授業に使用しているそうです。 きれいに配置することで、安価ながらモーターの仕組みがよく分かる模型の完成形に思えます。 |
| すごく魅力的な姿です。 |
| 逆上がりコマの動作原理 (井階さん、佐野さん) |
前回、安原さんが話題提供してくれた坂上がりコマですが、動作原理についての議論が前回の例会で白熱し、井階さんと佐野さんがそれぞれの考えを発表してくれました。 | |
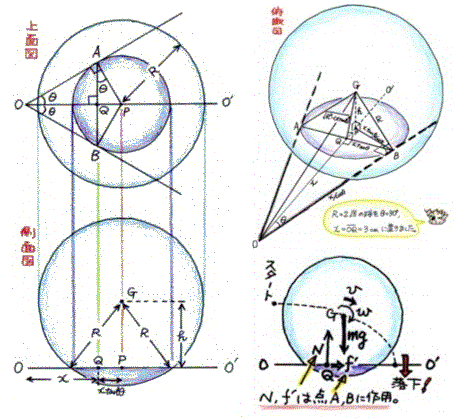
| まず、井階さんの考えです。半径R
の球を点A、Bで頂角2θのレールに接するように置き、OQ=xと
します。PQ=xtan2θであるので、回転軸AQBに対して変位xに比
例するmgxtan2θの回転モーメントが生じます。 球の慣性モーメ ントは(2/5)R2mなので、(2/5)R2m×(dω/dt)=mgxtan2θ。滑らない場 合の重心の速さはv=√(R2-(xtanθ)2)×ωで、はじめは摩擦力が、後には重力が支配的になって加速すると考えられます。 重心の軌跡は楕円を描き、接点の長さAQ,BQが Rcosθ を越えると、回転しながらストンと鉛直下向きに落下すると考えられます。 エネルギー保存則の観点から考えると、重心は位置xに比例、レールからの高さに反比例する割合で下がるので、一旦動き出した球は落下しきるまで止まりません。重力のみが作用する運動なので、(1/2)mv2 + (1/2)Iω2 + U = 一定 が成り立ち、重心が下がることによる位置エネルギーの減少分が並進・回転の運動エネルギーに変わると考えられます。 |
 |
前回の議論ではエネルギー保存則では納得いくのの、動きだしについて、重心がどこにあるのかがまとまらなかったため、佐野さんは、静止したコマが回転をしないとしても、また摩擦力が働かないとしても滑り出すであろうことから、①動き出す理由②回転し始める理由 に分け、運動を分析しました。 まず、①動き出す理由ですが、動き出すには、力が必要であり、重力は進行方向に成分を持たないため、コマがレールから受ける垂直抗力が進行方向に成分を持つからと考えました。 | |
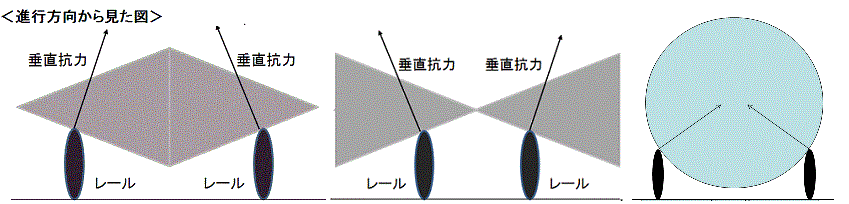 | |
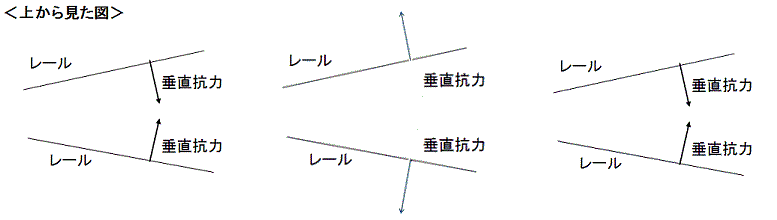
そこで、垂直抗力を進行方向からと上から図示すると、垂直抗力が進行方向に成分を持つことが分かります。 この合力が進行方向に動き出す原因ではないかという考えでした。 | |
 | |
| ピタゴラコースター (伊藤政さん) |
| 伊藤さんは向陽高校で行った文化祭の取り組みを報告してくれました。 ピラゴラスイッチを参考にしたコースターです。 時々、実践を見ますが、迫力を出し、再現性を担保するには、生徒の能力とかなりの指導者側の助言が欠かせないように思います。 伊藤さんの指導の下、一見の価値のある作品が完成しました。 |
 |
| 生徒達の達成感も大きかったことでしょう。 |
| ペットボトルの音 (伊藤政さん) | |
 |
一昔のコカコーラのペットボトルが叩くとよく共鳴することはサークル内ではよく知られていますが、倍音が実際に発生するのか杉本さん考案のトランペットスピーカーを使ったクントの実験機を利用し、コカコーラの共鳴を調べてみました。 <参考> ウイスキーのビンでクントの実験 (杉本さん) |
| 確かに倍音にすると、スチロール球がモードをつくり激しく振動します。 | |
| まず、発信器の振動数を少しずつ上げていくと、基本振動からスチロール球が一山でき、共鳴が見られました。
次に、振動数を上げていくと、スチロール球が確かに2倍音のような二山のモードをつくり激しく振動します。 二山のときの山の間隔12㎝が1400Hzの波長の1/2(半波長)になり、これがちょうどボトルを吹いたときの基本音の1つになるとのことです。 |
 |
| これを見せるだけでも、楽しめると思います。 | |
| ペットボトルを吹く場合は、ペットボトルのように複雑な形状だと、ボトルの口でヘルムホルツ共鳴が起こると考えられ、簡単に扱えないと経験者は語られておりましたが、今後の発展が楽しみですね。 |  |
| 複数の経験者によると複雑な形状では共鳴は難しすぎるとの事でした。 | |
| 「新科学対話」と比例中項について (井階さん) | |
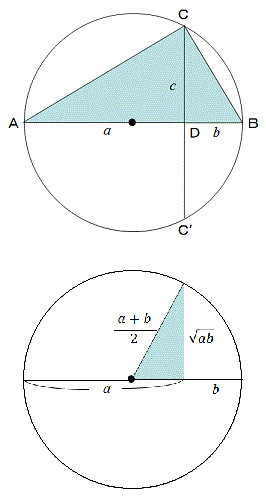
| ガリレオ・ガリレイの「新科学対話」は、ガリレイ物理学の総まとめであり、広範囲の力学を扱っています。 しかし、読んでみると説明や証明が極めて幾何学的で、代数学に慣れた私達には難解に感じるものです。 本文中に何度も登場する「比例中項」という言葉が分からなかったので、いくつかの辞書、辞典にあたったところ、①「相加相乗平均のこと」②「a:x=x:bのxのこと」と2つの定義が出てきました。 ①は、(√a-√b)2≧0から(a+b)/2≧√abと導かれる式ですが、幾何学的に考え、a+bを直径となる円を描くと、右の図1のように円周が(a+b)/2、円周上の点から直径に下ろした垂線が√abとなり、「三角形の斜辺は他の辺より長い」という自明のことを意味することが分かります。 ②は、図2において、△ACD∽△CBDより、a:c=c:b→c=√abとなるようなcのことです。 |
 |
|
科学史に明るい人からは、ガリレオの時代の科学書が幾何的なのは、ニュートンの時代までは幾何学が数学の王様であったことが影響しているとの意見がありました。 出版不況が叫ばれる中、文字離れや少子化等出版業界にはそれほど明るい話題はありませんが、このような基本的な書物が本屋から消えることに不安を抱いているとのことでした。 |
 |
| 今では絶版です。 |