２０１５年５月１６日の記録の第２ページです

　マグヌスカップ　（川田さん）　　

　先日の科教協のお楽しみ実験広場で岡田晴彦さんが紹介してくれたアインシュタインクラブ寺町さんのマグヌスカップ。

　マグヌスカップとは紙コップ２個の底と底をくっつけ、輪ゴムを何個かつなげたゴムを巻き、マグヌス効果で回転を生じさせるもので、そこそこ知られているもののようです。

＜外部リンク＞　マグヌスコップ

　川田さんはより正確に容易に発射できるよう、輪ゴムは耐久性のあるゴム紐にし、安定感のあるマグヌスコップの発射台を作りました。 　
　ゴム紐を丁寧に巻いては発射準備です。
　この発射台の向きを変え発射すれば、カーブ、シュート、フォークなど様々な軌道を描きます。

　演示用に使えそうです。
　発射台には緩衝材も張り付けてあります。
　コリオリ力の証明　（川田さん）　　

　

　コリオリ力とは慣性系に対して、一定速度ωで回転する座標系において、運動する物体にはたらく見かけの力のことです。

　台風の渦や、偏西風の起こる原因ともなっています。個人的には地理の授業で、２地点の最短航空経路について疑問に思い、先生に理由を伺ったことをよく覚えています。

　さて、川田さんの説明です。
　水平方向コリオリ力は影響がないので、点Ａでの角速度ベクトルωを鉛直成分と水平成分に分け、鉛直成分ωsinφの影響のみ考えます。
　地学で学ぶコリオリ力の説明です。
　点ＡからＢに辿り着くのにかかる時間⊿t ＝ ⊿l/v0
　⊿xをコリオリ力Fcによる等加速度運動と近似し、等速円運動の速度×時間とともに式を立てます。
　⊿x ＝ Fc/2m・⊿t2 ＝ ⊿lωsinφ・⊿t
　 ∴　Fc ＝ 2mωsinφ・⊿l/⊿t
　　　　　　＝ 2mvω0sinφ（∵v=⊿l/⊿t）
　と導けます。

　これが簡単かどうかは、近似を使うにはセンスが必要ですので、個人差が大きそうですが、すっきりしていてエレガントに違いありません。 　
　ＡからＢまで進む最短経路は図のように曲線になります。
　線密度と弦の振動　（川田さん）　　

　川田さんがテストに出題したという弦の線密度と弦に生じる定常波の波長の関係を考える問題です。

　ジグソーで振動を起こし、振動数を変えることで、定常波を作ります。弦の中央で一方は紐を４本束ね、弦の線密度が４倍となっています。また、滑車を通して、錘がつけられており、張力を一定にします。
　このとき、紐１本の方と、４本の方でできる腹の数はどうなるでしょうか？

　川田さんが模範解答としたのは線密度４倍なら波長が半分になるという下の図ですが、いざやってみるとなかなか定常波ができません。
　定常波をつくるのにジグソーを少し引っ張り、張力を連続的に調整する必要があり、張力も一定となっているのかも定かではありません。
　振動で錘までも暴れてしまいます。

　また、定常波の節が線密度の変わる境界から少しずれたところにができることもありました。

　弦の線密度の変わる境界での反射等も影響しそうです。線密度の境界が節になるような正確な実験が待たれます。

　テスラコイルで音楽再生４　（臼井さん）　
　音楽プレーヤーから入力された音声電流に、回路で900kHzのＦＭ変調をかけ、増幅したものを１次コイルに流します。それを２次コイルで高電圧に変圧し、その先端につけた導線から放電させます。

　２次コイルのもう一方の端は装置の裏にコンデンサーとして隠された貼られたアルミホイールに繋がっています。
　放電の火花が音声信号によって振動し、それが空気を揺らすため、音声となります。

　臼井さんがＡＭラジオを取り出し、900kHzに合わせると、なんとラジオから読経の声が・・・

　ＦＭに変調をかけたのに、なぜＡＭで拾えるのかと議論になりました。
　　前回は不調でしたが、ついに臼井さんの問題意識が共有されました。
　
　臼井さん所有の低い周波数も受信可能なＦＭ受信器を使うと、924kHzで音声を受信できました。
　また、放電が消えても聞こえるため、ＦＭの方は２次コイルじゃなくて、１次コイルから出ているのを拾っているんじゃないかという意見もありました。 　電磁波で通信しているのか磁場で通信しているのかをはじめ、意見はまとまりませんでした。

　そこで、井階さんが物理室のラジオチューナーをＦＭ受信してみると、大音量でクリアに音を拾いました。70MHz～90MHzの範囲のチャンネルではどこでも音を拾ったので、高調波ではないかという意見も出ていました。

　愛工の付近で混線した方がもしかしていらっしゃるかもしれません。怪しい宗教団体ではありませんので、お許しを！
　こちらは画像ですが、仮に図示するとなると大変ですね。

　力、速度、加速度のリアルタイム表示ソフト　（植田さん）　
　教員経験もある植田さんは、生徒がつまづきやすい運動方程式や力の向き、加速度等を分かりやすく教えたいと考え、物体に生じる速度・加速度ベクトル、さらに力ベクトルをリアルタイムで表示するソフトウェアを開発し、試作版を見せてくれました。

　カメラで黄色を認識するようにしたため、テニスボールを物体として使用する仕様です。
　色と位置を認識し、前後何コマかの位置の変化で速度ベクトル、加速度ベクトルを計算し、ベクトル表示します。
　勿論、力は重力を決め、加速度から求まる合力からの逆算で計算しています。
　何コマかの平均を取っているため、厳密なリアルタイムの計算ではないため、張力が糸の向きになる等の表示では使えないことなど様々な改善を期待します。
　プログラミングの技術を使い、精力的に活動されています。
　目の前での実験がモニターに示せるのは魅力的です。 　物の動きと表示には若干時間差があります。

　スペクトル分析のソフト　（伊藤政さん）　
　中村理科から出ている光のスペクトル解析ソフトを入手しました。

　単スリット回折格子を通過させ、ＣＣＤで検出します。電気信号の大きさと光度が比例するため、スペクトル解析を行うことができます。
　測定範囲は400nm～800nmの範囲で、透過光だけでなく、自動計算をすることで吸収光の分析も表示できます。

　伊藤さんは光源として白熱電球を使い、セロファンや透明下敷きのフィルター性能を調べました。
　装置の概要です。
　結果は意外にも色セロファンよりも下敷きの方が、色のフィルターとしては性能が良いようです。

　伊藤さんの実験によると緑のセロファンの吸収スペクトルは植物に近いことが分かったので、今後いろいろ実験を進めてみたいとのことでした。

　一校に１台あれば様々な面白い実験をやることができそうですね。
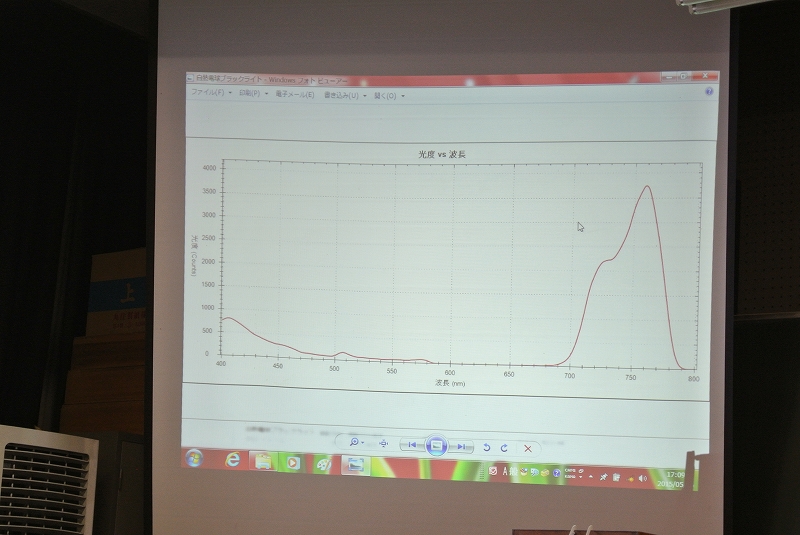　処理時間は短く、リアルタイムでスペクトル解析ができます。

　回折格子を使った万華鏡　（山本さん）　
　前回の光源が明るすぎて直視しづらかったのを改良し、光源からの光をピンホールで絞るようにしました。
　単体でも、らせん状に見える回折格子が入ったスペクトログラスと通してみると、下の写真のように綺麗な模様が観察できます。

　参加者から購入先を問われたスペクトラグラスですが、同じようなものを集めている山本さんにはどこで買ったのか記憶が残っていませんでした。
　これだけでも面白いスペクトログラスです。
　
　万華鏡を通すとたくさんのスペクトルが観察でき、賑やかです。

[前ページへ]