
2015年5月16日(土)愛知工業高校での例会の記録です。

2015年5月16日(土)愛知工業高校での例会の記録です。
| 放物運動の軌跡を見る (前田さん) |
| 教科書等に載っている「斜方投射の連続写真を肉眼で観察したい」というのが動機になり装置を開発しました。 斜面の前に付けられているのが塩ビパイプを加工して作ったビー玉の打ち出し口です。 |
 |
| 水平投射だけでは面白くないので、エコラップではねかえらせます。 | |
| 等間隔でビー玉を発射するために、ギヤボックスを使い、ギヤはボールを押し出すように形状を加工しました。
回転速度を一定に保つため、電源も直流安定化電源を用いています。 なるべく短い間隔でビー玉を発射するように、調整を行いましたが、誤作動等を鑑みると、現段階では0.2秒ごとにビー玉を発射するのが限界でした。 |
 |
| ストッパーを外し、定位置に入った玉をギヤで押し出す仕組みです。 | |
背景を白くするなどし、球を打ち出してみると、理屈通りの放物線が確認できます。 写真に撮ってみると、打ち出しの誤差があったり、ビー玉の間隔が広すぎてあまりよくありませんでした。 残像が残り、きれいに確認できるのでしょうか?肉眼で見ると、球は水平成分は等間隔になり、放物線を描いていたよう思えました。 電源が乾電池ではダメなのかとの質問が出ました。若干、誤差は増えるでしょうが、人の認知を考えれば、若干の打ち出す間隔の違いは許容範囲となりそうにも思います。 乾電池できれば、随分手軽に実験もできますしね。 |
 |
| エコラップではねかえり、箱に次々とビー玉が入っていのは爽快です。 |
| エネルギーとは? (林正さん) |
| 初学者にもエネルギーの概念を掴んでもらうために、正さんはエネルギーの定義について、提案を行いました。 「すべてのものが持っており、やり取りしても全体の量は変わらず、それによってお互いの状態が変化するもの」というのが正さんの考えた定義です。 これには、「これは保存量の定義で、運動量でも電荷でも何でも使え、エネルギーに限定できない」という意見が出ました。 正さんは「すべてのものが持っており」という表現がエネルギーはすべてのものが0ではないということを表そうと考えていましたが、若干、分かりにくいかもしれません。 |
 |
| 正さんの提案に対し、活発な議論が行われました。 | |
| さらに、重力による位置エネルギーなどのポテンシャルエネルギーは、基準を決めないと表せない相対的なものなので、この表現では含むことができないのではとの指摘もありました。 飯田さんは、教科書等の記述でもある「仕事をする能力」を使い、エネルギーの変換は様々な仕事を介さないとできないのではと意見を出しましたが、すべてがそれで解決するかは自信を持てませんし、かなりミクロとマクロの世界を横断した高度な理解が必要になる部分が出てきます。 |
|
| 縦波の横波表示(佐野さん) |
| 縦波の変位と位置のグラフを教えますが、思ったほど生徒の理解が進みません。 そこで、安価なプラスティックばねを使って、班でグラフから粗密の場所を探すという活動の紹介です。 「一人ひとり、等間隔に担当する点を決め、ばねを持ちます。」 「そして...。」 物理サークルではよくある光景ですが、佐野さんの指示を聞かずして、全員が持つ前にすでに何人かがばねを動かしてしまっています。やり直しです。 |
 |
| スタンドでばねを長く伸ばした状態で固定し、真下にグラフを置きます。 | |
| ばねが一様に伸びた状態で各自担当する点を持ちます。次にグラフの変位に従って、持っているばねを移動させます。 すると、粗密が生じる場所が視覚的に分かります。 |  |
| 密になるのは変位が0のこの点です。 |
| 立方体に内接する正四面体(奥村さん) |
| 奥村さんの同僚である数学の先生が、いくら口で説明しても理解できない生徒のため、立方体の頂点に隣接する3点を通るように切り取ると内接する正四面体を作ろうと、展開図を作成したそうです。 実際作ることで、イメージが湧きます。 空間図形としてとても興味深い内容ですね。 |
 |
| 「面白いものは買う」メンバーが多いため、飛ぶように売れました。 | |
 |
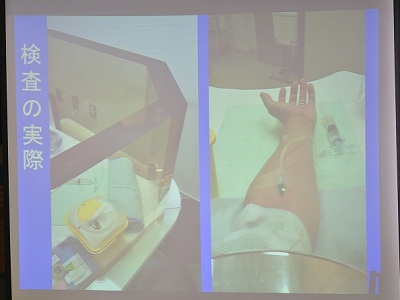
| PET-CT検査(井階さん) |
| 井階さんは、癌を患われ、しばらく休職されていました。 その間にPET-CT検査を受けられましたが、その検査の説明に加え、なんと検査時の内部被爆、外部被爆量などを見積もり、報告してくれました。 PET-CT検査とは、陽電子を放出する核種を用いて、非侵襲的に腫瘍の様子を探る検査です。 癌がブドウ糖を多く消費するという特異性に着目し、フルオロデオキシグルコースを癌細胞に取り込ませ、癌細胞が活動するとそこで放射線を発するため光としてとらえることができます。 |
 |
| 簡単な構造ですが、作ってみて気付いたことも | |
| 検査を受けるのに、滅多にないチャンスと、井階さんは愛用の放射線量計での測定を計画しました。 積算の放射線量を測ると、ほんの数分で0.1mSvを超えてしまい、普段との線量の違いに恐ろしさを感じるほどでした。 井階さんの計算によると、検査での被爆総量は約7mSvで、18F-FDGによるものが1〜2mSvほどだったそうです。 また、18F-FDGの管理についても、豊田の管理施設から名古屋の病院まで、放射線量の変化を見越して、輸送を行っていることなど、色々な裏話も楽しまれたように感じました。 井階さんは4月より、担任に戻られました。様々な経験を経て、井階さんの教育への情熱が生徒の心を揺さぶることでしょう。 |
 |
| この状況でも冷静に状況を楽しもうとしていた井階さんです。 | |
 |
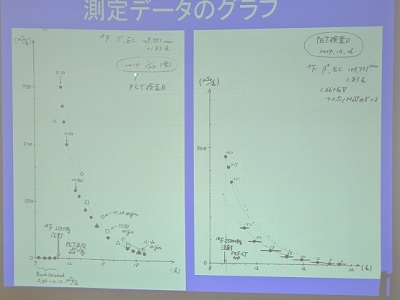 |
| 手持ちの線量計ではすぐに積算が最大値に達してしまいました。 | 放射線量の時間変化から半減期も計算してみました。 |
| 振動で進むブラシ(飯田さん) |
| 前回、振動ブラシの進む方向について、議論になりました。 これについてサークル通信では、モーターの回転に対する反作用のトルクで垂直抗力が増し、最大静止摩擦力も比例して増えるため、右下の写真の左側のように回転するとの井階さんの解説がありました。 |
 |
| ブラシをハンマーで叩くとき、進む向きは何で決まるか? | |
| それに対して、飯田さんはブラシをハンマーで叩いた時にブラシの叩かれた側が凹むような瞬間的な現象の効果が卓越する可能性を捨てきれずにいました。 例会では、飯田さん持参のデジタルスケールを使い、振動を起こした際の、実際に垂直抗力の変化量を測りました。 |
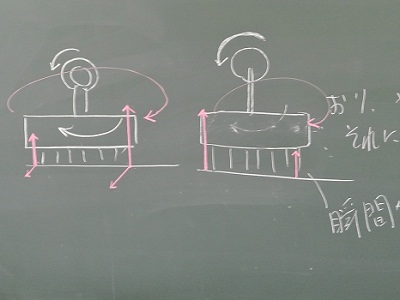 |
| 飯田さんの疑問は、瞬間が効くのかそれともそれ以外の時間が効くのか。 | |
 |
結果はご覧の通り、2つの目盛の和が0にならないのは少し気になりますが、井階さんの説明通りになりました。 飯田さんはすぐに納得し、司会で次の話題に進んだため、その後の実験結果は把握しておりませんが、愛工の同種のスケールでより正確な実験及び、議論は続いておりました。 |
| 2つが違うのは、家にあったのがこの2つだったため。飯田さんらしいです。 |
| 五重塔の免震構造 (飯田さん) |
| 前回に続き、五重塔の話です。 まずは、五重の塔が安定する理由は、建物が1階でなく、5階あるからではないかと投げかけました。 1階建の牛乳パックに振動を与えると、激しく振動します。2階建て以上にすると、激しい揺れが収まりました。 3階建て以上でも同様に建物の揺れは収まります。 次に2階建てで1階に筋交いを入れると1階は振動しない代わりに2階が激しく振動します。 この結果から、飯田さんは五重の塔の1階が免震構造の役割を果たしたのではないかと結論付けました。 |
 |
| 1階建てでは激しい振動を起こすと、勿論激しく揺れますが。 | |
| ただ、模型は五重の塔と構造が同じとは言えません。柱がない面で支える構造で、2面は壁がないこと、基礎をないものとして扱っていることなど、ひっかかるところがあるのも事実です。 |
 |
| この構造では2階建て以上で揺れは劇的に軽減。 | |
| 次に、2つのお酒の箱を振動させました。 すると、片方は激しく振動しましたが、もう一方はほとんど揺れません。 中を見ると、空箱に天井から棒がつってありました。 これが前回紹介した振動のエネルギーを吸収する心柱の効果です。 |
 |
| 心柱が共振したとき、床の損傷で建物の倒壊を防ぐ考えなのでしょうか。 | |
| さらに五重塔は建物が傾いた場合には、屋根が大きく重いことにより、重心にかかる力が復元力となるモーメントを生むという説明もありました。 確かに少し傾くと確かに復元力は生じますが、重心が支点より高いので傾きが大きくなると倒れるのを助長してしまいます。また、五重の塔は上の階ほど部屋は狭いので、力のモーメントでううでの長さは減ります。 これらの事がすべて意図して作られた物なのか、偶然の産物か、分からないところもあるようですが、震災にも耐えてきた建築の構造に学ぶことも必要ですね。 |
 |
| 五重塔が興味深い対象であるのは確かです。 |
| 霧箱 (林煕さん) |
霧箱の改良に余念がないひろさん。定量化を可能とし、稼働時間を増やすべく、底にあるエタノールをダンボール紙と黒ラシャ紙に染み込ませ、アルコールを循環させることで、小型なものでも2kgのドライアイスで15時間ほどの動作が可能になりました。 |
 |
| 薄いステンレス板を加工し、熱伝導の良い受け皿を作りました。 | |
 |
ひろさん手持ちの減塩しおを近づけると、飛跡が一気に増えました。これは減塩しおには放射性カリウムが含まれていることに加え、霧箱がとても高性能であることが原因です。 より簡単に作れる小型霧箱の作り方は公開されています。自由研究等の格好のネタとなりそうですね。 <外部リンク> 名古屋大学F研 霧箱の作り方 |
| 減塩しおを近づけると、多くの飛跡が現れました。 |