
2016年2月13日(土)愛知工業高校での例会の記録です。

2016年2月13日(土)愛知工業高校での例会の記録です。
| 運動の授業の映像教材製作 (植田さん) |
| 物理サークルに参加している教員は演示実験等を行っている人がほとんどのため、実物を見せる方が効果的であるという声が当然のごとく大きくなりました。 しかし、現場では実験が行われていないことも多いように聞きます。 何もやらないよりは映像で見るだけでも、自然現象の手助けにはなるはずです。 |
 |
| 自作のソフトを使った映像教材を開発中です。 |
| 実験の物理量リアルタイム表示 (前田さん) |
| リアルタイム表示の装置がメーリングリストで話題になったので、島津の既製品を使った演示実験例を紹介してくれました。 この装置では、位置、速度センサーに2台の超音波距離計が使われており、6、7mの距離まで反応するそうです。 例会では、実験例として質量が異なる台車の、衝突前後で運動量保存則を示す実験を行いました。 |
 |
| 青く見えるのが超音波距離計です。 | |
| 右の写真のように、実験後すぐにグラフを提示できるのは魅力的です。 道具は使い方次第ですが、しっかり設問を組み立てれば、物理の概念形成に効果的に使えるようにできそうですね。 |
 |
| このようにグラフが表示されます。 |
| p-vグラフの可視化 (前田さん) |
| 前回、土肥さんが紹介した装置を前田流にアレンジしました。 主な改良点は加熱に使うドライヤーをバイク用のヒーターに変えたことです。 繰り返しドライヤーでペットボトルを温めると、ペットボトルが変形してしまったことからこのように工夫しました。 温度センサーも付けてみましたが、音の高さで圧力変化をつかむ土肥さんのアイデアの方が面白いと思い、最新版では使用をしていないそうです。 |
 |
| バイク用のヒーターの方がペットボトルが傷まないそう。 |
| コインでだるま落とし (前田さん) |
年明け最初の授業で、生徒全員にコインを使ってだるま落としを体験させました。 10円玉や1円玉を積み上げ、トランプで連続してコインを飛ばします。 衝突のコツをつかみ、リズムよくやるとすべてのコインが飛んでいきます。その様は爽快です。 |
 |
| これは、熱中してしまいます。 | |
| 100円ショップで手に入れただるまの頭を乗せると、本格的になり、難易度も増すそうです。そうに思いました。 |  |
| 雰囲気作りも大切。ちょうどいい大きさのだるまも用意しました。 |
| 速度の向きが変わる運動 (前田さん) |
速度と時間の学習で、躓く生徒が多い速度の向きが変わる運動を作り出せないかと缶を使って、作り出しました。 見かけは普通の缶に見えますが、これを転がしてみると、途中で戻ってきます。 |
 |
| 中はどうなっているのでしょうか? | |
中身はどうなっているかとの問いが前田さんからありましたが、さすがのサークルメンバーの面々。 ズバリ、仕組みを的中させました。 中には、ゴムに錘が吊るされており、ゴムをねじって、戻る復元力を利用しています。 |
 |
| 錘がゴムでつながれています。 |
| 共振とうなり(石川さん) |
| 前回、共振はうなりであるという話をしてくれた石川さん。振り子の共振は互いに逆位相の状態と言えますが、石川さんが撹乱をあたえ、うなりの状態(互いの位相差)を変える方法を見つけ紹介してくれました。 |
 |
| 前回紹介できなかった石川さんの実験が紹介されました。 | |
| 石川さんは共振振り子の一方の振り子の錘りを磁石とし、コイルで磁場をかけ、振り子の見かけの重力を増やすという方法を考えました。
実際、磁場をかけ続けてみると、定常状態を変えることはできませんでした。 そこで、磁場をかけるのをうなりの周期に合わせてON-OFFしてみました。 すると、同位相の状態から逆位相の状態に徐々に移行していきます。 |
 |
| 磁場をかける装置です。 |
| 定時制での生徒主体の授業(佐野さん) |
| 定時制90分の授業実践の中で特に生徒の満足度が高かったものを紹介してくれました。 1つ目は、情報過多なこの時代に、生徒に何を教えるべきかを考え、行うことにした対照実験の授業です。 前半では、対照実験の方法を学びます。まずは、実験を行う上で結果に影響する物理量を考える練習や結果と考察の違い理解に努めます。 後半では、実際に対照実験の考え方を使い、「ラジオメーターを回す方法をできる限り多く見つけ、回る理由を考察する」という課題を4人の班で取り組ませます。 |
 |
| 課題の提示はプレゼンテーションで行っているそう。 | |
| 授業では簡単な説明の後に生徒を外に連れ出し、日陰の近くの日向で解散するようにしています。 このような授業で大切なのは教師が教えないこと。生徒の発見の目をつまないよう、励ますこと褒めることのみ行います。 生徒からは、はじめは「風で動くのかな」という意見なども出てきますが、対照実験を意識させることで「光で動くのではないか」という意見や、日陰のアスファルトの上でも良く回ることを見つけ、「熱が原因だ」とか、「黒が熱を吸収して黒側が押されたように回っているのでは」とかいう意見も出てきます。 さらに、追加の実験として「冷やしたらどうなるか」という意見や、光か熱かをはっきりさせるため、熱だけを与えようと「ドライヤーで熱風を送るとどうなるか」など実験のアイデアも出てきます。 また、「底を擦ると回る」という予期しないような答えも出てきたそうです。 |
 |
| ラジオメーターの原理を探る探究的な実験。 | |
| 次は、奥村さんに教えてもらった「円周率を測る」実験を誤差や有効数字の学習とセットで行った実践報告です。円が書かれた様々な大きさの紙を用意し、それを使って円周率をなるべく正確に求めることを課題とします。 計算が苦手な生徒も多いため、やる前は不安もあったそうですが、事前に円周率の定義をしっかり確認し、生徒に求められれば、定義の説明を繰り返し行う事で授業を上手く回すことができました。 初めはなかなか手が動かない生徒も、紙を何等分かに紙を切って、円弧を直線に近い形とし、長さを測ったり、糸を使って長さを測り、定規と合わせることで実測化したりと工夫が出てきます。 中には、全く話ができない生徒もおり、不安があったそうですが、アンケートではそのような生徒も満足度が高かったそうです。生徒たちが達成感を味わうことがこの結果を生んでいるのでしょうか。 |
 |
| 円周率を求める実験では円周率の定義をしっかり確認しています。 |
| 浮力と力の関係(井階さん) |
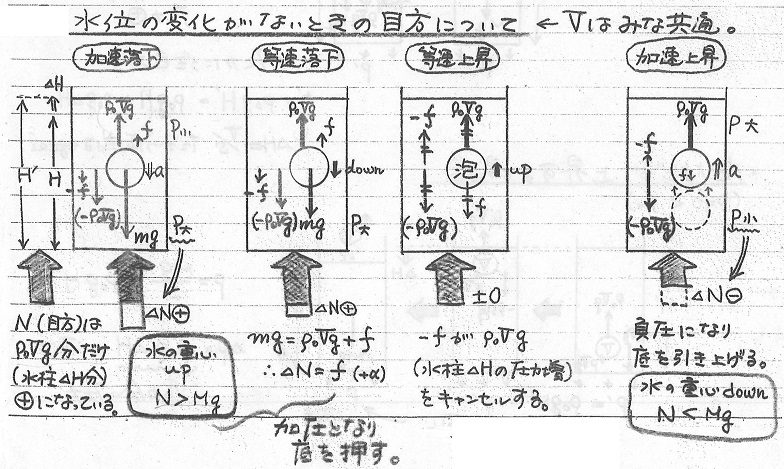
| 前回、結論が出ずに終わった、林さんの泡の上昇とはかりの目方の実験結果を、追加実験を行い、理論的に解析してみました。 まずは、気中共鳴の装置の一端に目盛のついたポンプをつなぎ、任意の体積の泡が上昇するときの、はかりの目盛を調べました。 すると、泡を入れると、瞬間的に重くなり、その後、元の重さつまり水+容器の重さになりました。 泡の大きさを変えてみると、泡が大きい方が目方の増加が大きく、目盛付きのポンプを使うことで泡の体積分の浮力の反作用分目盛が増えたのではないかというのが井階さんの見解です。 |
 |
| 緻密に実験計画を練り、定量化に成功しました。 | |
| 次にフラスコを泡と見なし、水中でのフラスコの浮上とはかりの目盛の関係を調べました。 このとき、ビーカーと水、フックの重さの和は2700g、フラスコとゴム栓の重さは33gです。 |
 |
| 上手く練られた実験です。 | |
 |
|
| 高校生による竜巻の研究 (伊藤 政夫さん) |
伊藤政夫さんが工夫した竜巻発生装置ですが、向陽高校科学部のメンバーが竜巻の発生原理とより優れた装置の開発を目指し研究を始めました。 煙をL字にしたストローで上向きにゆっくり送る、障害物を置いて流れの変化を調べるなどし、竜巻の発生条件を調べました。また、空気を送る柱の数を変え、比較実験を行うなどしました。 |
 |
| 伊藤さんの実験を生徒が研究テーマに。 | |
| 竜巻の中心部が気圧が低くなっており、向心力が生まれることにより、竜巻が山のように上に行くほど中心に近づいた形になっている事、床面で空気の回転ができないと竜巻ができないことなどが分かりました。 |
 |
| 煙をつかって風の流れを調べました。 |
| 高校生によるジャイロの研究 (伊藤 政夫さん) |
もう1つのグループは、ジャイロ効果について学び、ジャイロ効果を利用したおもちゃ等を模倣したり、作り出したりしてきました。 |
 |
| こちらはジャイロ効果の研究です。 | |
中でも、ジャイロクレーンは非常にユニークで面白い作品です。 |
 |
| このクレーンで荷物を移動させることができます。 |
| 複雑な運動(川田さん) |
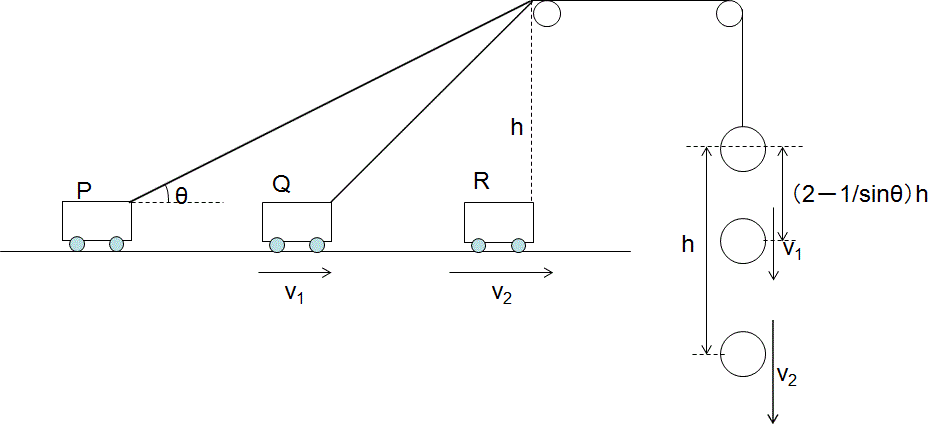
川田さんがテストのために難しめの(高校生には難しすぎる?)問題を考えました。そこで考え付いたのが、以下の問題です。 なめらかな床の上にひもとつながれた質量Mの台車が点Pに静止している。張られたひもは2つの定滑車の先にあるおもりとつながれており、質量m(<M)のおもりは動かないように支えられている。このとき、台車が点Q、Rに達した時の台車とおもりの速さV1,v1,およびV2,v2を求めなさい。 ただし、滑車は十分小さく、ひもとの接点は変わらないものとする。 |
|
 |
|
| この答えを川田さんは、A.力学的エネルギー保存の法則 B.運動方程式 の2パターンで解きました。 A. 力学的エネルギー保存の法則より、 mgh(2-1/sinθ)=1/2MV12 ―― ① V1とv1の関係より、 v1=V1cosθ ―― ② ①②より、V12=2mgh(2-1/sinθ)/(M+mcos2θ) ―― ③ v12=2mgh(2-1/sinθ)/(m+M/cos2θ) ―― ④ B. 運動方程式は 台車 MA=Tcosθ ―― ⑤ おもり ma=mg-T ―― ⑥ 加速度の関係より a=Acosθ ―― ⑦ ⑤⑥⑦より、A=mgcosθ/(M+mcos2θ) ―― ⑧ また、 a=mg/(M/cos2θ+m) ―― ⑨ この結果を吟味すると、③④と⑧⑨に整合性がありません。一体、どこで間違ってしまったのでしょうか?? その後、検討を重ねると、加速度の式⑦が間違いではないかということになりました。では②がは正しいのになぜ⑦が誤っているのか? それは②の右辺にあるVだけでなくcosθも時間tによる関数であるからです。 |
|