２０１５年９月１２日（土） 　点と点を線で結んで数学しよう！ −グラフ理論の世界へ− 中村　啓介 先生（京都府立桃山高等学校）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　講座で使用するワークシート
　　いくつかの点と点を線で結ぶと図形ができますよね。その図形を使って遊んでみましょう。
　　一筆書きなどの色々なパズルを考えながら、図形に潜む数学を考えてみましょう。

お薦め本：『数学オリンピックチャンピオンの美しい解き方』　テレンス・タオ (著), 寺嶋英志 (翻訳) (著) 　青土社　　　　　

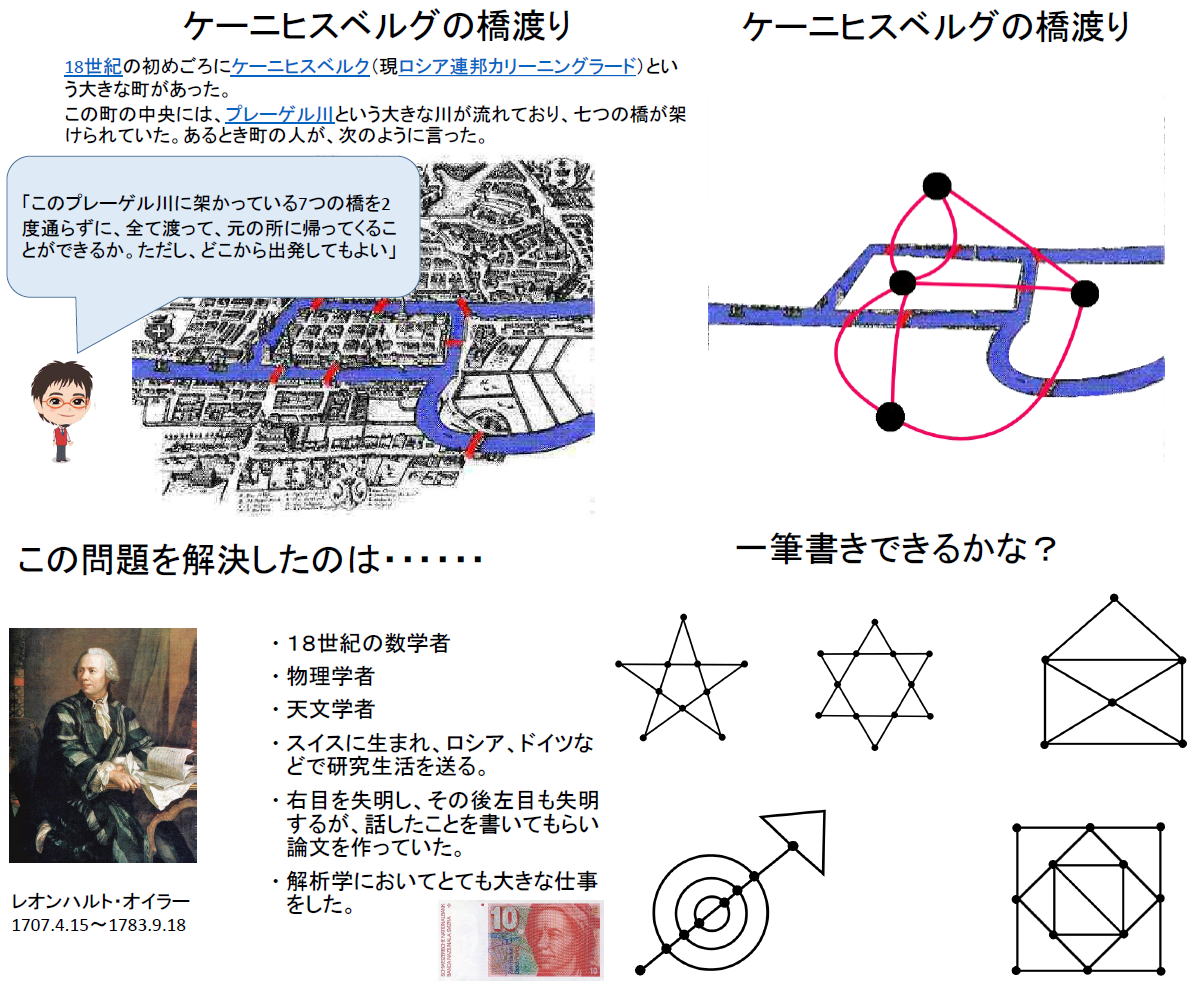
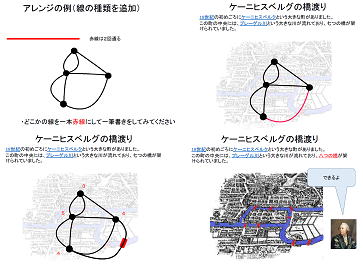
後期がスタートしました。宣伝する時間と募集期間が 短かったのですが、それでも参加総勢40名でした。 関心が高くて頭が下がります。	一筆書きの導入として、「ケーニヒスベルグの橋渡り」の問題を考えました。この問題の解決を示したのはレオハルト・オイラーそこで、一般的な一筆書きのできる図形について取り組みました。	スタートできる点に着目して、点を通る線の本数を調べて みることがヒントです。図の点上に、線の本数を書き込ん で、特徴を考えてみましょう。一筆書きのできる図形を見 抜くことができるはずです。ワークシートを用いてみまし ょう。

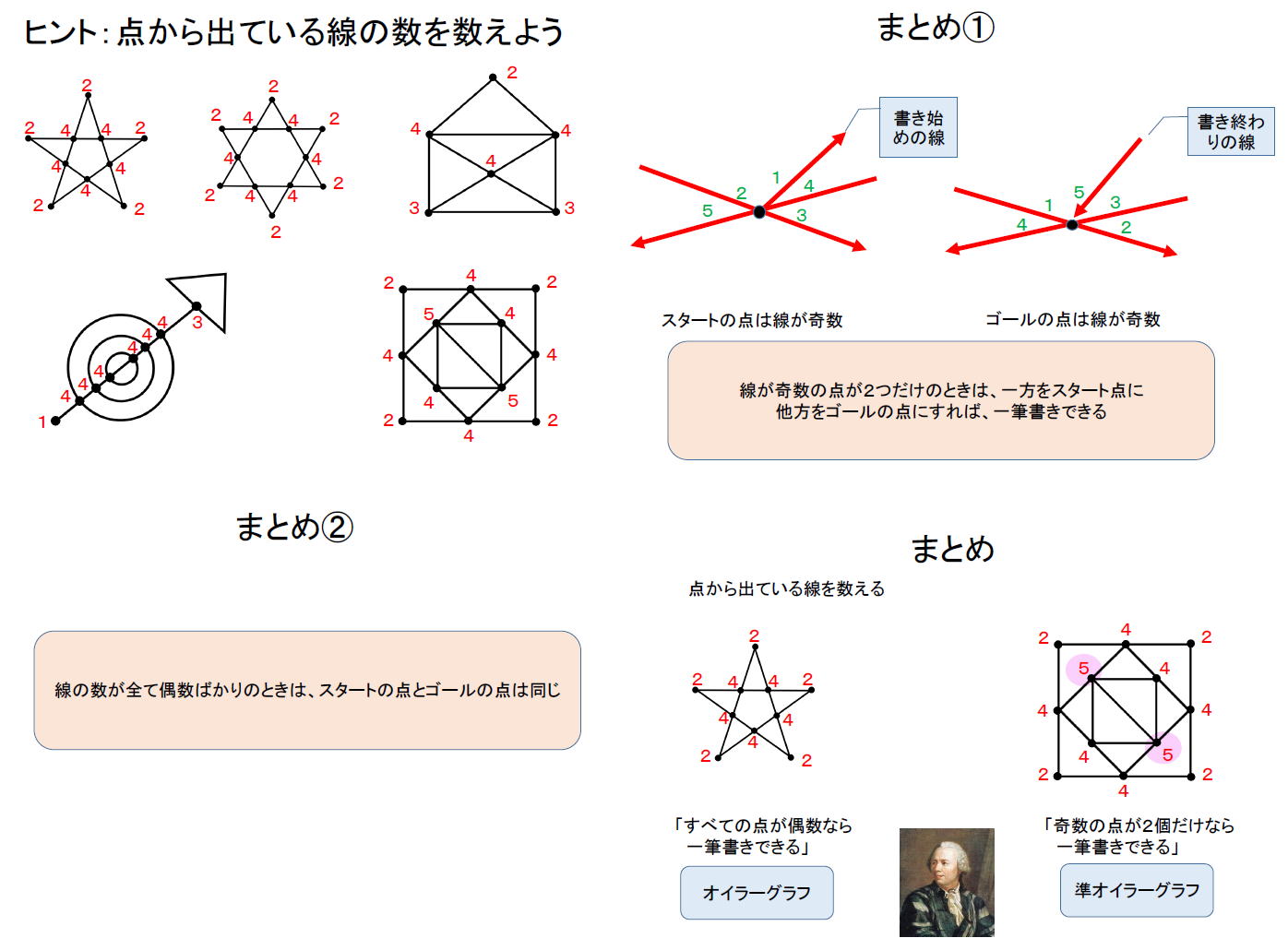
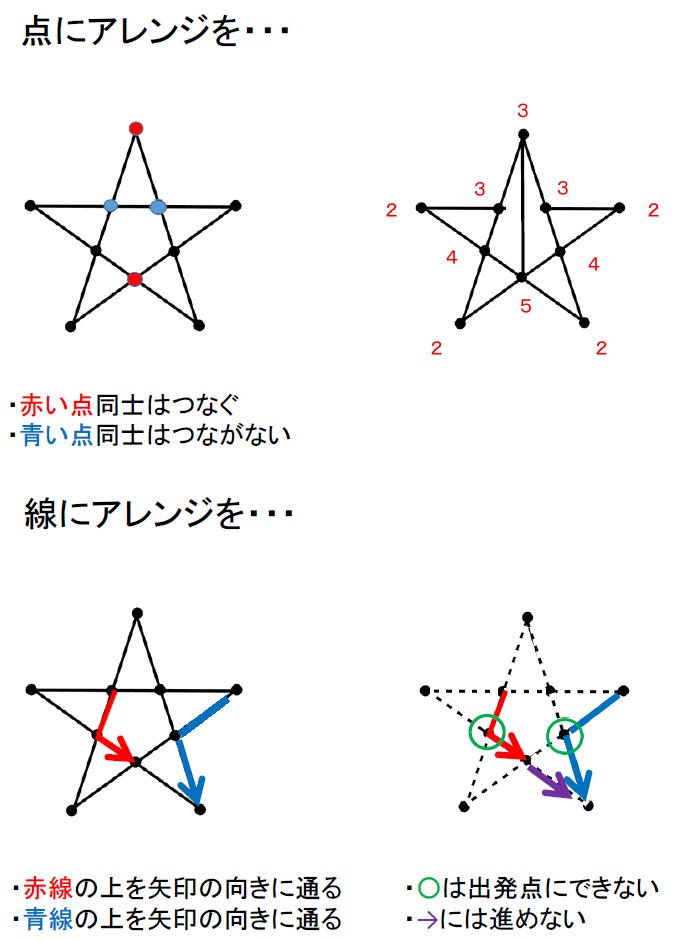
点から発進している線の本数が、偶数本数ならばその点は通過点にもなります。しかし奇数本数あるならば、その点は出発点か終着点にしかなれません。	ということは、ワークシートの５つの図形は一筆書きできるの でしょうか？オイラーグラフと準オイラーグラフという名が付く のですよ。指でなぞって、考えてくれています。	全て図形が一筆書きできることが分かった後は、新ルールを作ってみました。図形上の2点を選んで赤色としたら結線、青色としたら断線とするとどうなるでしょう。また線に→を付けた場合は、どうなるでしょう？

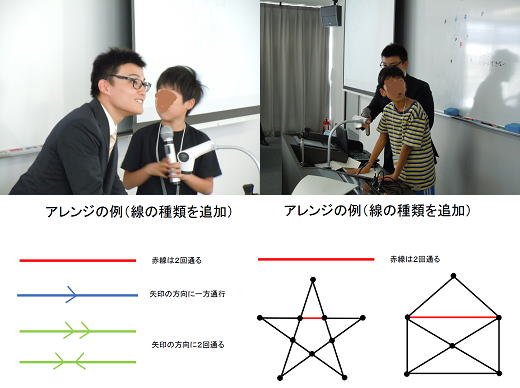
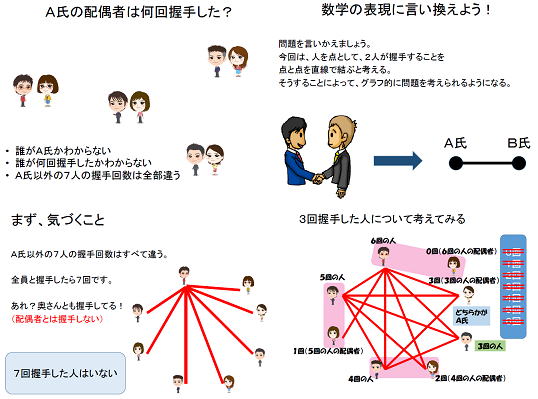
京都教育大学の弘田真基さんに講師をバトンタッチ。受講生に ルールを変えて、色んな一筆書きを発案し、解法を述べてもらい ました。	そのルールをケーニヒスベルグの橋の問題に当てはめて橋を1つ作れば、2度橋を渡らなくても元の位置に戻って来れますね。	グラフを作って、組合せを考える別の考えましょう。

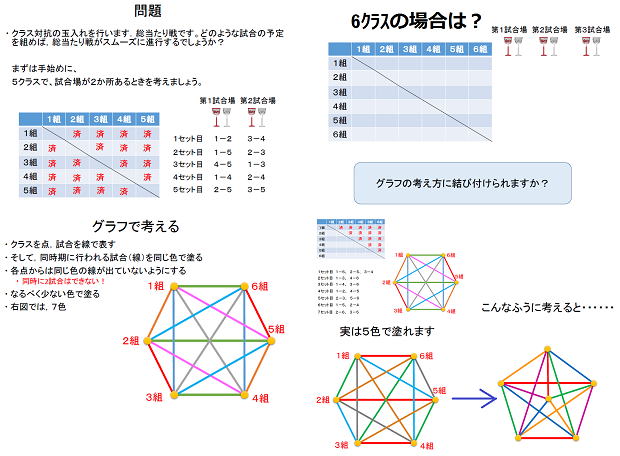
この説明を見て、答えが分かるかな？	玉入れの対抗戦を考えます。５クラス対抗の場合と６クラス対抗の場合とで、総当たり戦をスムーズにする方法をグラフを使って作りましょう。	色ペンを用いて、最後の一踏ん張り！！  　　　　　　　　　　　　　　　　　　　　　　　　これでお終いです。