２０１９年 ６月 １日（土）  いろいろな立体を作ろう 花木　良 先生　　（岐阜大学）

　　　　　　　　

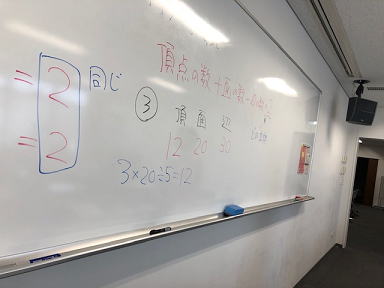まずピラミッド（正四面体）とサイコロ（立方体）を作って、 頂点と面と辺の数を数えます。それぞれどのような関係が あるか発見します。続いて正２０面体を作ってみます。	どうやら （頂点の数）＋（面の数）−（辺 の数）＝２の関係のようである。	これをオイラーの公式というのですが、面の数から頂点の 数を求める方法に何か良い手がないかと尋ねたら、写真 のような明答をした参加者もいました。
次にサッカーボール（切頂２０面体）の形を作って、オイラ ーの公式があてはまるか確認します。	先程の正２０面体の頂点部分を 色塗りしますと、サッカーボール になるのです。	サッカーボールの頂点や面や辺の数の数え方を工夫して 正２０面体との関係をつかんでみましょう。（双対多面体）