

交流回路実験器
湘南台高校・山本明利
交流回路における、抵抗、コイル、コンデンサーの各素子のはたらきを手軽に示すことのできる装置を製作した。設計のポイントは、各素子のリアクタンスをそろえて、オシロスコープでの定量観察をしやすくしたことと、接続がわかりやすいように回路図にあわせて配線したシースルーの基板を用いたことである。
抵抗は任意の抵抗値のものが容易に入手できる。コンデンサーも容量の数値が限られてはいるが比較的種類が豊富で選ぶ余地がある。しかし、コイルは種類が少ないので、まずコイルで手頃な大きさのものを決め、それにあわせてコンデンサーが巨大にならないような周波数レンジを選択し、コンデンサーと抵抗の数値を決定するという方針で設計した。
結論として、コイルは手頃な大きさで比較的入手しやすい40mHを選択した。交流周波数10kHzに対するリアクタンスは
ωL=2πfL=2×3.14×104×40×10−3=2.5kΩ
となる。当然、20kHzに対しては5.0kΩである。
一方、コンデンサーに対しては、周波数依存性がコイルと逆になることを強調したいので、10kHzで5.0kΩ、20kHzで2.5kΩとなるようにする。そのためには規格で入手しやすい3300pFのものを用いれば10kHzに対して
1/ωC=1/2πfC=1/(2×3.14×104×3300×10−12)=4.8kΩ
と、目標に近いリアクタンスになる。コイルもコンデンサーもこの前後のものが適当で、このランクをはずれるとコイルまたはコンデンサーのいずれかが大きくなり、レイアウト上美しくない。
各素子の大きさと、基板レイアウトは左下の写真の通りである。接続をわかりやすくするためあえて切り替えスイッチは用いず、バナナプラグとバナナジャックで素子を選択するようにした。各素子に流れる電流を検出し、位相差を観察するため、直列に10Ωの抵抗(写真下方茶色の素子)を入れてある。この抵抗値は抵抗、コイル、コンデンサーのリアクタンス、2.5〜5.0kΩに比べて十分小さくなければならない。さもないと、コイル、コンデンサーのときの位相角が90゜からずれてしまう。ただし、信号源の低周波発振器の出力から予想される電流に対し、電圧降下がオシロスコープで十分検出できる程度でなければならないので、1〜10Ω程度とするのが適切である。
実験観察は発振器、周波数カウンタ、二現象オシロスコープを右下のように接続して行う。


それぞれの素子の、周波数10kHzと20kHzの交流電圧に対する電流応答をオシロスコープで観察した結果を下に示す。いずれの写真でも、振幅の大きい波形が入力電圧(スケールは1V/div)を、小さい波形が電流応答(スケールは10mV/div)を表している。水平方向のスケールは25μs/divである。電流の振幅の周波数依存性と電圧に対する位相変化が教科書通りになっているのがよくわかる。
| f=10kHz | f=20kHz | 一定の振幅の電圧に対する電流応答 | ||
| 抵抗 | R=2.5kΩ | 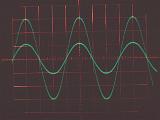 |
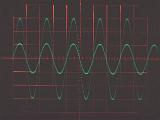 |
電流の振幅は周波数によって変化しない。 電圧に対する電流の位相の遅れはない。 |
| R=2.5kΩ | R=2.5kΩ | |||
| コイル | L=40mH | 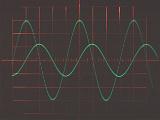 |
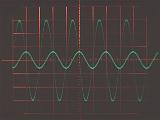 |
電流は周波数に反比例して小さくなる。 つまりリアクタンスは周波数に比例する。 電流の位相は電圧に対して90゜遅れる。 |
| ωL=2.5kΩ | ωL=5kΩ | |||
| コンデンサー | C=3300pF | 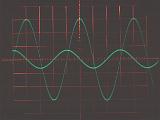 |
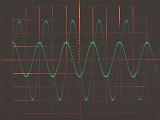 |
電流は周波数に比例して大きくなる。 つまりリアクタンスは周波数に反比例する。 電流の位相は電圧に対して90゜進む。 |
| 1/ωC=5kΩ | 1/ωC=2.5kΩ |
素子の組み合わせとしては次のような候補もある。コンデンサーを2個並列というところがスマートではないが、各素子の入手は比較的容易で、オームの法則の暗算がしやすいのがメリットである。
| f=5kHz | f=10kHz | ||
| 抵抗 | R=1.0kΩ | R=1.0kΩ | R=1.0kΩ |
| コイル | L=33mH | ωL=1.0kΩ | ωL=2.1kΩ |
| コンデンサー | C=8200pF×2並列 | 1/ωC=1.9kΩ | 1/ωC=1.0kΩ |
高等学校・物理(清水書院)指導書(現在絶版)に掲載の記事をリライト
99/03/14 YPCニュースNo.132掲載