先日NiftyServeのFKYOIKU【理科の部屋】で、数研の3TRIAL物理の電界と電位の問題の解答がまちがっているのではという記事がありました。正負の等量でない電荷が作る電界で、両電荷を通る直線上で電位０（無限遠基準）の点はどこにあるかという問題です（当該の問題ではＡが＋３ｑ、Ｂが−ｑ、ＡＢ間の距離がｒという想定）。
うちの学校でもこの問題集を使っていたので、ちょっと調べてみたら、確かに解答の不備で、解答には二つある該当する点のうち一つしか載っていないのでした。まあ、よくある話だと思います。その件については「解答の不備ですよ」とコメントをつけて落着したのでしたが・・・
この問題は数研の他の問題集にも収録されていて（数研はこの手の使い回しが得意ですね）、調べてみると正解を載せているものもあるのです。それもけっこう古い問題集に。どこでどうまちがった「遺伝情報」が書き込まれたものか興味があります。まあ、それもさておき・・・
誤答の著者は教科書の説明図によく載っている、正負等量電荷の場合が頭にあって、勘違いをしたものと思われます。この問題を考えているうちに、一般には正負の（等量でない）電荷Ａ、Ｂが作る電界で、電位０の点はＡＢを通る直線上に２箇所存在するのが普通だということに気が付きました。しかし・・・
簡単のために二次元の電界で話をすると、正負の点電荷の周囲の等電位線は楕円に似た閉曲線になります。したがって、この等電位線とＡＢを通る直線との交点はＡＢの間に１箇所と、どちらかの外側に１箇所と普通は２箇所できます。電位０の等電位線もその一例と考えてよいはずです。ただ一つの例外は、正負電荷の絶対値が等しい場合で、このときの電位０の等電位線は線分ＡＢの垂直二等分線になってしまいますから、交点は１箇所しかできません。Ａを取り巻く閉曲線からＢを取り巻く閉曲線へ移り変わるちょうど境目の特殊なケースにあたるわけで、それがこの場合たまたま電位０なのです。当該の問題は正負等量ではないのでこの場合にあたりません。
とNiftyには書いてみたものの、これはあんまり厳密ではない。あらためて考えてみました。図１は
のグラフをLotus1-2-3に描かせたもので、直線ＡＢ上のポテンシャル曲線に相当しますが、水平な等電位のレベルで切るとＶ＝０〜約0.5のときは交点が４箇所できます。この区間は同じ電位の等電位線が２本の閉曲線になるからです。それを除けば「普通は２箇所」でよさそうですが。
図１この問題のように、大きい正電荷と小さい負電荷が並んでいる周辺でのポテンシャルは、例えていえば、富士の裾野にすり鉢状の井戸を掘ったようなもので、全体としては正の高さの土地が圧倒的に多い中に、ただ一箇所、負電荷の周辺だけ海水面より下に達する深い穴があいているようなイメージです。断面でみればこの井戸の近傍に２箇所海抜０メートルの点P、Qができます。この２点が解答の点です。
さてそこで問題です。
(1)この電荷分布における等電位線を描け。
(2)正負等量電荷の場合の電位０の等電位線のように、等電位線が直線または開いた曲線になってしまう電位が、正負等量でない場合にも存在するか。
これらはＹＰＣの例会で投げかけて宿題にするつもりが、例会での議論の中であっさり結論が出てしまいました。まとめると以下のとおりです。
正負等量でない２電荷の場合は、電気力線の一部が両電荷を結ばず、無限遠方をめざします。この問題の例では、ＡＢ間の距離が無視できるぐらい十分離れたところから見れば、＋３ｑ−ｑ＝＋２ｑの点電荷があるのと同じに見えるはずで、Ａから出た電気力線の３分の２はそこから放射状に無限遠をめざし、これと直交する等電位線はその電位が０に近付くにつれ、電荷のある位置を中心とする同心円に近付くことになります。したがってすべての等電位線は必ず閉じなければなりません。直線や開いた曲線になる等電位線は絶対に存在しないというのが結論です。
そして電界が０になる場所は、直線ＡＢ上のＡＢの間でないところ（絶対値の小さい電荷の側）に、必ず１点、それもただ１点、鞍部点として存在するということになりそうです。この問題の例では
という点がそうです。図１では点Ｒになります（ｒ＝１の場合に相当）。
以上のようにみてくると、正負等量２電荷のケースは、直線の等電位線が存在し、電界が０の点は存在しないという極めて例外的な電荷分布ということになります。
問題(1)の答えは、定性的ですが上記の議論をふまえて描くと下図のようになるものと思われます。ＡＲＵＧＡの線画図形の描写力ではこの辺が限界です。
図２【参考文献紹介】本件に関しては必見の関連情報があります。神川定久さんのＪＡＶＡアプレット「電気力線」では、二つの点電荷の電気量比を変化させながらコンピュータの描く電気力線をインタラクティブに観察できます。ここをクリックしてさっそく見に行きましょう。
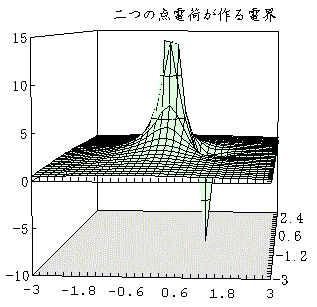図３ Excelで描いた電位の立体図。【ＹＰＣニュースNo.81掲載】
【後記】発端となった3TRIALの解答はその後訂正され、現行の問題集には正しい解答が載っています。
一つ前のページへ
ホームページに戻る