(3)均衡を破る機構 (4)綱引き必勝法 追記
(1)静力学的な考察
下図は綱を引いている一人の選手のつもりです。この人に外部からはたらく力のつりあいと大小を考えて、綱引きに勝つための条件を考察しましょう。最初は簡単のため、静力学的に考えます。つまり「ゆさぶり」のような激しい動きははないものとし、つりあいに近い状態で、敵味方がほぼ互角に引きあっているものとします。

外部から人にはたらく力は4つあります。手が綱から受ける摩擦力T(他にも味方がいる時はTは綱の張力ではないので注意)、足が地面から受ける垂直抗力N、足が地面から受ける摩擦力F(N,F合わせて抗力と呼んでもよい)、そして人が地球から受ける重力mgです。縄の重さも一人当りならたいしたことはないのでmgに含めて考える事にします。
上下方向には運動が起こらないものとすると、つりあいの式
N=mg
が成り立ちます。問題は水平方向の力です。相手に勝つためには言うまでもなく
T<F
であればよいわけです。この選手が後退運動を起こすための条件です。Fは静止摩擦であれば、最大摩擦の条件 F≦μN を満たさなければなりませんから、
F≦μmg
となって、摩擦係数μが大きいほど、また体重が重いほど、足が滑りにくく、摩擦力FやTの上限を増すことができ、有利である事がわかります。これは経験的にも明らかです。
一方、手が綱から受ける摩擦力Tは、その反作用である手が綱を引く力の味方チーム全体についての合力が敵チームを引く力となりますので、T自身もできる限り大きい方がよいわけです。T<Fであればよいからといって、手を放したり、手が滑ってTが小さくなれば、自分は後退できますが別の意味で負けになります。Tも最大摩擦の条件を満たさなければなりませんから、摩擦係数をμ'、握力をN'として
T≦μ'N'
が、手が滑らないための条件となります。摩擦係数μ'が大きいほど、また握力が強いほど有利なのは言うまでもありません。
敵味方の勢力が拮抗している時には、上記3つの不等式の不等号は限りなく等号に近く、ぎりぎりのところで勝負が行われていると考えられます。
(2)体の回転運動に関する考察
次に、姿勢を崩さないように引き続けるためには、体の回転、とりわけ前方へつんのめることを避けなければなりません。足と地面の接点Pを中心にした力のモーメントMを求めてみます。つまさきと体の重心を結ぶ線分PGの長さを半角文字でPGと表すことにします。PGと地面のなす角をθとしましょう。同様につまさきと手(綱からの力の作用点)を結ぶ線分PSの長さをPSとし、PSと地面のなす角をφとします。θとφは通常は比較的近い角度でしょう。「勝つ」方向への回転を正とするために、図1で時計回りを正として力のモーメントを求めると、
M=mgPGcosθ−TPSsinφ
となります。M<0となると前方へつんのめって負けます。
Mを正にするためには、mとPGを大きくし、θ、PS、φは小さくするのが望ましいことになります。ここでも体重は大きい方が有利です。PGを大きくするために足はなるべく伸ばすのがよく、しゃがむのは不利です。θ、φを小さくするために、からだは適度に後方へ傾けます。ただしFを稼ぎやすい姿勢はありますのでこれは程度問題。最後に、PSをなるべく小さくとるために、綱からの力の作用点を下げるとよいことになります。「綱は腰で引け」というのはこれのことでしょう。肘を曲げて腰に近い位置で引く方が有利だと考えられます。
上の考察は選手が姿勢を崩さないための条件として議論してきましたが、もっと積極的に、人間のからだをてこにして重力から綱を引く力を発生する機構と解釈してもいいと思います。Pが支点、Gが力点、Sが作用点というわけです。
「同じ体重ならお尻が重いより頭が重い方が有利」←本当かなあ(^_^)
(3)均衡を破る機構
今度は、綱引きをしている敵味方の選手を、綱もろとも一つの物体系と考えることにします。手と綱の間にはたらく力はすべて内力となります。上下方向の力はつりあっているものとして除外すると、つまるところ、この物体系にはたらいているのは地面からの摩擦力だけと考えてよいことになります(図2)。綱引きは単純化して考えると、この摩擦力の大きさを競う競技です。
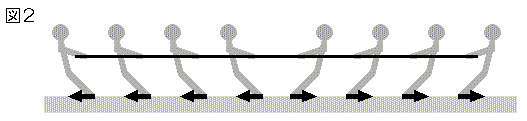
足が地面から受ける摩擦力は、足が地面に及ぼす力の反作用になりますから、上図の向きになり、この力をより多くかせいだ側に系全体が動くことになります。
仮に敵味方の力がほぼ拮抗している状態を考えましょう。つまり、両方向の力がつりあって静止している場合です。このつりあいはどうやって破れるでしょうか。
第一に考えられるケースは、負ける側がほとんど足を滑らせてしまい最大静止摩擦から一気に運動摩擦になって大幅に摩擦力を減らす場合。このときは摩擦力の差が5〜10%程度になると考えられるので、かなり大きな加速度での地滑り的な決着を見ることでしょう。こういうケースはあまりないようですが、幼稚園や小学校の運動会で見かけることがあります。
ある程度の年齢になると、知恵がついて、足が滑りそうになると無意識に踏み替えをして最大摩擦を保とうとします。運動摩擦の方が小さいことを体が知っているわけです。そう簡単に姿勢を崩すこともありません。この場合ですと、多少動き出しても摩擦力の大きさは大きく変化しないと考えていいでしょう。
仮に敵味方50人ずつ、計100人が綱引きをしてつりあっている時に、一方の選手の一人が力尽きて引くのをやめたとします。あるいは他方の誰かが突然二人分の力を出しても同じことですが、100人もいる中で一人分ぐらい差があっても大勢に影響ないような気がしますが、はたしてそうでしょうか。
一人の人が綱を引く力をほぼその人の体重程度と考えましょう。(1)の考察から足が受ける摩擦力も最大摩擦に近ければこれと同程度です。悪い近似ではないはずです。上の状況では双方の力の合力が一人分の体重程度になり、この力で100人の人間と綱という物体系を動かすことになります。つまり、大まかに言って一人で100人を動かすことになりますから、ちょっと考えるとびくともしないという印象があります。
しかし、運動方程式を立ててみればわかるように、この物体系には重力加速度の100分の1程度の加速度が生じます。10cm/s2程度の加速度です。わずかなようですが時間をかけると、1秒で5cm、2秒で20cm、3秒で45cm、4秒で80cm・・・程度の運動を生じることになります。はじめはほとんど動いていないように見えますがあきらめずに引いているうちに次第に速度が増してきます。
上記のような議論が的を得ているのかやや不安ですが、一般の綱引き競技のよく見かけるラストシーンはこんな感じに見えませんか?大まかに見積もって全体で一人分ぐらいの力が勝敗を分けているのではないかと思うのです。したがって選手の一人一人が、「自分一人の力でも100人を動かせるんだ」と信じてあきらめずに引き続けることが勝利への道であるというのはいかがでしょうか。
スペースシャトルの乗員は船外活動で、何トンもの人工衛星を人力で動かしたりします。慣性がありますから、無重力(正しくは無重量)だからといって軽々と動くはずはないので、じんわりと力を加えながら時間をかけて動かすのだと思います。100人の人間の体重は5〜6トンでしょうか。人工衛星が動かせるなら、100人だって動かせるはずですね。
(4)綱引き必勝法
以上を「綱引き必勝法」としてまとめましょう。さあ、これでクラスを勝利へ導こう!\(^o^)/
1.できるだけ体重の重い選手を抜擢する。‥‥‥(mを大きく)
2.滑りにくい靴を履く。 ‥‥‥(μを大きく)
3.握力を鍛え、綱をしっかり握る。 ‥‥‥(N'を大きく)
4.手に滑り止めを施す。 ‥‥‥(μ'を大きく)
5.しゃがまずに足を伸ばす。 ‥‥‥(PGを大きく)
6.からだは曲げずに後方へ傾ける。 ‥‥‥(θ、φを小さく)
7.肘を曲げて腰に近い位置で綱を引く。 ‥‥‥(PSを小さく)
8.最後まであきらめずに引き続ける。 ‥‥‥(何事も気合が大切!)(^^)
なお、綱引きでは全身の筋肉を緊張させますが、これはからだをこわばらせて、座屈(棒などが圧縮力に抗しきれずに折れ曲がる現象)に耐える意味が一番大きいと思います。

