例会速報 2026/02/15 関東学院中学校・高等学校・Zoomハイブリッド
YPCホームページへ| 天神のページへ| 他のサークル・団体等へのリンク| 次回例会のご案内
YPC例会のもようを写真構成で速報します。写真で紹介できない発表内容もありますので、詳しくは来月発行のYPCニュースで。例会ごとに更新します。過去の例会のアルバムはここ。
授業研究:教職課程の実験 西尾さんの発表
西尾さんは遠隔参加で、薬科大学での教職課程の物理の授業を紹介してくれた。
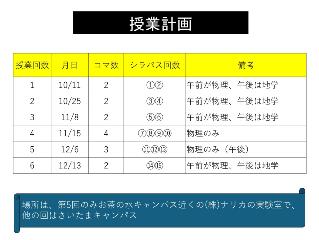
今年度の後期、「中高理科の教職課程の学生実験」を初めて担当した。90分15コマで、2~4コマの連続授業として全6回である。大学に物理実験器具がなかったこともあり、PCやスマホ、簡単に入手できる材料などで行える定性的な実験を主として扱い、市販の実験器具を使った実験はナリカの実験室を借りて中学教科書の物理実験を実施した。西尾さんが今回報告したのは、このナリカでの実験以外の概要である。
初回の1コマ目はガイダンス、受講の心得、安全指導、 PC・スマホとインターネットの実験への活用がテーマで、安全指導では西尾さん自身が過去に経験した失敗事例を具体的に紹介した。
教科書は順天堂大学の医療系学部の2名の教員と科学写真家の伊知地国夫氏による「身近な素材で実験する物理」で、タイトル通り百均などで入手できる材料による手作り実験が基本で、医療系らしく「身体を使った体感できる実験」が多く載っている。実験前の予想のディスカッション、実験、結果の考察、物理法則の確認、例題、という流れで書かれており、学生が教育実習などで実際に授業を行う際に活用できるものとして選定した。


実施した実験は、上記の教科書の実験、それ以外の身近な素材でできる実験、スマホやPCを活用できる実験である。


教科書以外の実験は、バランスフォーク(2020年2月例会で発表)などの手持ちのネタが主だが、理科教室2025年8月号に詳しく作り方が紹介された林式霧箱(右図)など、今回初めて実践してみたものも含まれる。ちなみにこの林式霧箱は、線源を入れなくても自然放射線がよく観察できる優れたものである。スマホ利用の実験は、APEJの「高校物理の授業に役立つ基本実験講習会」の自由落下・水平投射の実験など、アプリ
phyphoxを利用したものをいくつか実施した。実験結果を写真や動画で報告させた実験も多いので、その意味では学生がスマホを活用する機会は多かった。


太陽望遠鏡 山本の発表
その昔、ナリカ(当時中村理科工業)のガレージセールで入手した直径40mmの平凸レンズ(左図)。平面ガラスの上に凸面を下にして重ね、ニュートンリングを観察するための試料である。この凸面の曲率半径は3mだと箱に表示されている。つまりとても長焦点(約6m)の凸レンズなのだ。これを黒いスチレンボードの中央にはめ込んで、日なたに出し(右図)、直焦点の太陽像を観察する。


太陽高度が高いときは鏡で光を水平方向に導く必要がある(左図)。レンズから6mぐらい離れた焦点位置に白い紙をかざすと太陽像が観察できる。太陽像の直径は6cm近く、黒点も観察できる(右図)。レンズの直径(40mm)よりも太陽像の方が大きいので、肉眼で直接太陽を見上げるよりも像の方が暗いので、危険はない。とはいえ、まぶしいので直視はしない方がよい。なお、安い鏡はガラスの裏面が銀面になっているため、ガラスの表面反射でずれた像が重なって見え、像がダブる。できれば表面鏡を使うとよい。


例会で実験した時刻は4時近くで、都合よく陽がだいぶ傾いてきたので、窓際にレンズを高く掲げてもらい、鏡を使わない直焦点でも観察してみた。すると、太陽像はくっきりとして、黒点もはっきり観察できた(左図)。
レンズの球面半径をRとすると、平凸レンズの焦点距離はf=R/(n-1)となる。光学ガラスの屈折率を約1.5とすると、Rの約2倍が焦点距離となる。この場合約6mだ。また、太陽の視直径は0.5°で、そのタンジェントが約0.01弱であることを覚えておくと、太陽像の直径は焦点距離の約1%弱で、およそ6cmとなることが概算できる。


複数所持していたので、会場で6枚を放出。久々の「とりジャン」で盛り上がる(左図)。「最初はグー・・・」
ところで、この実験に使用した鏡は、前日にダイソーで購入したスタンドミラー(スクエア)(サイズ:16.7cm×20.8cm×6cm)、220円。表面は普通の平面鏡だが、裏面は焦点距離約65cmの凹面鏡になっていて、ご覧の通り夕方の日差しでも紙に火がつく(右図)。収斂火災の恐れがあるので絶対に日なたにおいてはいけない。生徒に扱わせる際も十分に注意したい。


プラコップスピーカー? 益田さんの発表
いわゆる「パスカル電線」と同じ原理で、LANケーブルをループにしたものを、オーディオアンプに接続して音声信号を流す。ケーブルのまわりには振動磁場ができている。これを、プラスチックコップに薄型ネオジム磁石を貼り付けただけのピックアップで受信する。磁石は二六製作所に発注したもので、直径2㎝、厚さ1mmの薄型ものだが、本当は発注をミスってしまったのだという。しかし、怪我の功名で、磁石が軽い分、振動を鮮明に受け取ってくれる。


磁石だけでも十分に振動を感じ、音になって聞こえる。ノーベル賞級の研究でもそうだが、「失敗は発明の母」なのである。なお、使用しているアンプは、100WのBluetoothアンプで、外部電源は必要だがお手軽に実験ができる。


東レの結果と新製品 中川さんの発表
中川さんは3Dプリンターで様々な教材を作って公表している。授業用に力学台車を自作し、マイコンと各種センサーをセットにした「スマートカートオプション」も開発してこの台車に搭載できるようにした。合わせて7000円の予算でできるという。さらに、台車に搭載できる「慣性力実験機」のオプションも開発した。スマホも搭載できるので、観測者の視点を変えて投射運動や、浮力の変化を観察できる。


下は、加速度運動中の浮力を観察している様子。浮きや素面の傾きが、台車に乗った観測者の立場でも明瞭に観察できる。これらの装置は惜しくも東レ賞の受賞を逃したが、中川さんはデータやノウハウを公開して普及をはかっている。


下の写真は、3Dプリンターで作った正負等量電荷によるポテンシャル面の立体模型。片側ずつ作って、一方を逆さにして貼り合わせるのだそうだ。


光学実験用の実験器具も3Dプリンターで作った。市販の光学実験セットは赤色レーザーしかないが、3色使いたいと思い、RGBのレーザー光源を固定できるホルダーを作り、ナリカの光学台に載せて使っている。


この実験のときに使用しているのが、左図の小型スモークマシン。6000円でおつりが来る価格だという。スモークを漂わせると、レーザー光線の光路がはっきり見える。


音の干渉の可視化 鈴木健夫さんの発表
鈴木さんは、この年末年始に、AI(Gemini)に「物理の授業に使える実験工作を提案してくれ」と相談した。いくつかの電子工作を伴う提案をされて試しに作ってみたあと、色々やりとりをした結果、「音の干渉の可視化実験」を再度提案され、それを作って実際に授業で使ってみた。
鈴木さんの説明によると、電子工作は、Arduino nanoを使って、マイクで音を拾ってその音の音量によりLEDを点灯させるというもの。Geminiは用意するものや回路、さらにはArduinoのプログラムまですべて具体的に提示してきた。物品はAmazonですべて調達。計4,000円くらい。電子工作を自分で行うことはほとんどなかったという。
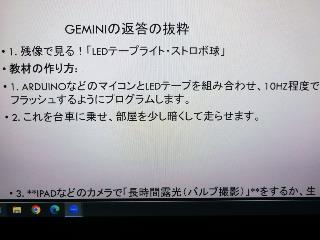
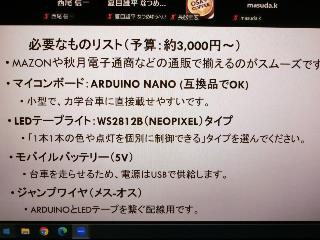
これらの工作がすぐにうまくいったわけではなく、何度も動かずに止まってしまったが、そのたびにGeminiにその症状を伝えて相談すると、「ここが不具合の可能性があるので、こうしたらよい」などと丁寧に答えてくれて、電子工作素人でも完成にたどり着けた。まるで近くに電子工作の玄人がいて折々にアドバイスをしてくれる、という感じだったという。
実際の授業では、教室(物理実験室)で2つのスピーカーから1000Hzほどの同じ音を鳴らし、片耳をふさいで頭を左右に揺らせたり教室内を歩かせたりして、音の干渉の様子を体感させるという定番実験の後、生徒の感想で「よくわからない」(音の強弱を自分自身が認識できない)という声があったので、次の時間にこの「可視化装置」を鈴木さんが持って歩いてLEDがついたり消えたりするのを見せる、という展開とした。「あくまでも補助的に理解を進めるというだけの効果だが、やってみる価値はあったと思う。」とは鈴木さんの弁。
Geminiのそもそもの提案はデジカメの長時間露光で、暗い部屋で歩いて回ると、双曲線の光の筋が見えてくるはず、というものだったが、デジカメの設定などがハードルとなり、できていない。鈴木さんはいずれ挑戦したいと思ってる。

滝川さんの静電気 越さんの紹介
越さんは、滝川洋二さんがFBで発信していた静電気の実験を紹介した。薄い半透明なポリエチレンの袋を10x15cm程度に切り、長い辺に平行に等間隔に4本程度の切れ込みを入れる(左図)。このポリエチレンシートとクリアフォルダをティッシュペーパーで擦り、負に帯電させる(右図)。


帯電したポリエチレンシートを上方に投げ上げ、クリアフォルダをポリエチレンの下側で受け止めるように水平に保っと、安定した形に広がった状態でポリエチレンシートを浮揚させることができる。米村傳治郎さん考案の「電気クラゲ」よりも簡単に静電気の反発による浮揚実験ができる。


Gemini(Googleの生成AI)の活用 益田さんの発表
益田さんは、最近Geminiでアプリを作成し授業で使っている。いくつかの指示を重ねて、HTMLで出力し、Google siteで生徒へ提示している。PhETでもう少し…と思うところを手作りすることや、教材に合わせてシミュレーションを作成することができる。提示する教材としても、生徒の触らせて学習させる教材としても活用の幅が広がりそうだ。生徒自ら作成させても面白いかもしれない。


また、Notebook lmはアップした資料のみを用いて、要約やスライド作成、練習問題作成を行ってくれるAIで、Google workspaceのコアサービスに入っている。
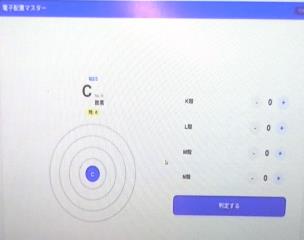
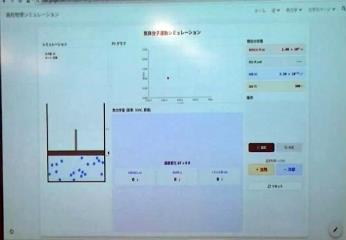
手書きのメモからもこんなみごとなスライドを作成してくれる。授業用のスライド作成がかなり早くなりそうだ。いずれ生徒が活用して…となりそうなものなので、私たち教員も積極的に触れておくべきだろう。
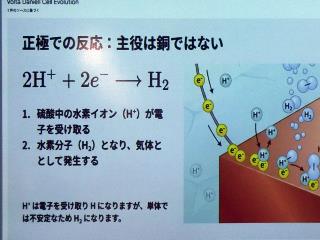

化学基礎の話 天野さんの発表
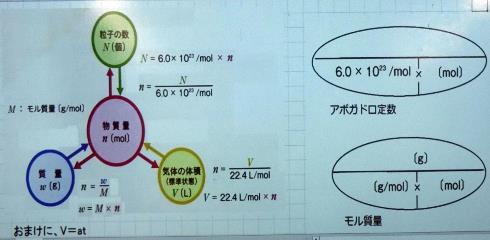
「距離=速さ×時間」による計算をいわゆる「はじきの方法」の暗記で教えることには批判があるが、天野さんは、計算が苦手な生徒でも、とりあえず問題が解けることで、「理科を嫌いにさせない」「あきらめさせない」効果があると考えている。
要するに「はじき」は、a=bcの関係がある3量を、Tの文字の横棒上にaを、縦棒の両側にbとcを配置すれば、求めたい量を指で隠すことで、他の2つの量からの計算方法を機械的に知ることができる便法である。天野さんは、今は化学基礎を教えているが、化学はこの類いの比例計算が多いから、同じ方法が使える。合わせて、単位に注目するように指導すると、より深い理解へのきっかけになる。単位算だけで進めようとすると、「分数」による割り算で立ち往生する生徒も少なくない現状があり、こんな教授法を併用しているという。

秋月電子通商のアウトレットコーナー 櫻井さんの発表
櫻井さんは、秋月電子通商秋葉原店2Fにあるアウトレットコーナーについて紹介してくれた。主に長期在庫品が通常価格より安価に販売されており、回路用の抵抗器に至っては、種類こそ限られているものの、1000本で10円(つまり100本入りの1袋が1円)という破格だった。櫻井さんは、例会の席で無料で振る舞ってくれた。
ここに並んでいるものは、総じて販売単位が大きかったり、クセが強い商品だったりするので、よく調べてから買わないと後悔するかもしれない。多くの人が手に取る売れ行き商品は長期在庫にならないはずだから当然だろう。


なお、八潮店にはジャンクガレージというコーナーが常設されており、こちらは販売単位の小さいものから並んでいる。店内陳列に使っていて古くなったバスケットが10円で販売されていたり、何故か炊飯器が2000円で売られていたりと、負けず劣らず混沌としていて面白いとのこと。どちらの店舗も、一度は訪れて自分の目で確かめてほしいと櫻井さんは語る。
実は櫻井さんはこの機に、PicoScope5203というPC用オシロを購入した。今回は発表の時間がなかったが、次にYPCに参加する際に紹介してくれるそうだ。


DeepLより高精度な翻訳サービスの紹介 櫻井さんの発表
 櫻井さんは、最近よく利用している「PLaMo翻訳」という翻訳サービスを紹介した。日本のPreferred Networks社が開発した大規模言語モデル「PLaMo」を活用したAI翻訳サービスで、日本語の学習データが豊富である点に特徴がある。2025年10月にサービスを開始し、WebページやChrome拡張機能を通じて以下のURLから利用できる。 https://app.translate.preferredai.jp/
櫻井さんは、最近よく利用している「PLaMo翻訳」という翻訳サービスを紹介した。日本のPreferred Networks社が開発した大規模言語モデル「PLaMo」を活用したAI翻訳サービスで、日本語の学習データが豊富である点に特徴がある。2025年10月にサービスを開始し、WebページやChrome拡張機能を通じて以下のURLから利用できる。 https://app.translate.preferredai.jp/
実際に使ってみると、従来のAI翻訳サービス(DeepLやChatGPTを用いた翻訳)と比べても、日本語がかなり自然で流暢であり、不自然さはほとんど感じられない。翻訳の精度や自然さはChatGPT5.2
Thinkingとほぼ同等でありながら、出力速度は圧倒的に速い。櫻井さんはその点が気に入り、最近では翻訳サービスとしてPLaMo翻訳をほぼ一択で利用している。無料プランでも文字数制限はあるものの、テキスト翻訳、Webページ翻訳、ファイル翻訳といった各種機能を利用できる。ぜひ一度、使ってみてほしいとのこと。
櫻井さんが、各種翻訳サービスで同じ英文を和訳して比較した資料(PDFファイル:229KB)はここ。
進路と学問をつなげるツールに向けて 中田さんの発表
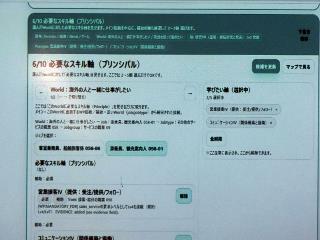
中田さんは「オシロビジョン」という会社を創業して、学習支援アプリの開発を行っている。今は、どんな大学に進めばいいか、どんな職業に就くべきなのかという、高校生の進路相談に乗ってくれるAIアプリを開発中だ。既存の進学/就活支援サイトとの違いは、様々な問答の中から利用者の適性を見いだすと共に、今すぐにできる一歩まで、目の前の道を示してアドバイスしてくれる点だ。
夢を実現するためには、どんなスキルが必要か、それを身につけるためにはどうすればいいかを示しても、当人が実践しなければ意味がない。今日できることから始めて、具体的なタスクに分解し、一歩ずつ順に先の道を示してくれる。生徒はそれをもとに、今の自分を見つめるとともに、将来までの行動計画を立てることができる。一方、教員側は生徒がどんな希望を持っていて、現在どう努力しているかを把握することができ、適切な指導につなげることができる。
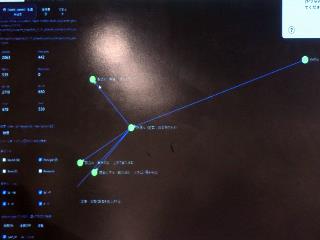
アプリの裏側で動いているのは、国が示している膨大な職業データと、生徒の生の声を集めたデータベースで、それらを結ぶものとしてスキルツリーを備えており、途中の経路を可視化できる。
二次会 黄金町駅前「しまちゃん」にて
 14名が参加してカンパーイ!例会本体には対面で22名、遠隔で4名、計26名の参加があった。本日の例会も発表内容が充実していて、全てのメニューをこなしきれなかった。学校会場だと実験室が使えるので、実験・実演が自由にできるのがよい。実験好きのYPCメンバーはいやが上にも盛り上がる。
14名が参加してカンパーイ!例会本体には対面で22名、遠隔で4名、計26名の参加があった。本日の例会も発表内容が充実していて、全てのメニューをこなしきれなかった。学校会場だと実験室が使えるので、実験・実演が自由にできるのがよい。実験好きのYPCメンバーはいやが上にも盛り上がる。
YPCホームページへ| 天神のページへ| 他のサークル・団体等へのリンク| 次回例会のご案内