前の月の例会｜ 例会アルバム目次｜ 次の月の例会
例会速報 2016/09/18 多摩大学附属聖ヶ丘中学・高等学校
ＹＰＣホームページへ｜ 天神のページへ｜ 他のサークル・団体等へのリンク｜ 次回例会のご案内
授業研究：測定値の不確かさ 宮崎さんの発表
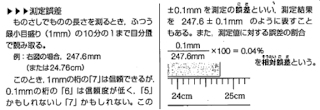
宮崎さんは、普段から疑問に思っていた「測定値の不確かさ」をテーマにして発表した。有効数字の授業のプリントの抜粋を紹介しながら、『測定値の不確かさをどう教えているか』『使っている教科書にはどう書いてあるか』を例会参加者にたずねた。
現行教科書の測定値の不確かさの記述には２種類ある。「最小目盛1mmの物差しでの測定値247.6mmは，±0.1mmの誤差。測定結果を247.6±0.1mmのように表すこともある。」という記述の教科書（左）や、「58.7mmという測定値、真の値は56.65~58.75mmの間にあるので、±0.05mmの誤差を含む。」という記述の教科書（右）がある。
例会参加者でも、あまり意識していない人が多いようで、使われている教科書にどう書いてあるか知らない人が多かった。ちなみに、参加者の学校での使用教科書を挙手で調べたところ、１位数研、２位啓林館だった。
宮崎さんは「不確かさの幅はどちらが正しいのか、２種類あっても良い理由を知りたかったのですが、ご存知の方はお教えください。」と、疑問を投げかけている。
ＡＡＡＡ電池 宮崎さんの発表
宮崎さんが使っているパソコンのデジタイザー・スタイラスペンの電池が切れた。電池を交換しようとしてあけてみたら、単４よりも径が小さい。調べると、通称単６、米国通称AAAAという電池だった。ヨドバシでも見当たらず、ネットで購入。でも高い！いろいろ調べてわかった乾電池の規格についても紹介があった。
さらにネットで調べてみると、「006Pの電池に単６が６本入っている」という情報があり分解してみた。（電池に禁止事項の記述があるので、決して真似しないこと。）
６Ｐは６層の意味だが、左の写真の左側のように積層しているものと、右側のように細長い（単６？）電池が６本直列につながっているタイプの2種類があることがわかった。
後者をケースから取り出して広げてみるとこんな感じで、確かに直列接続になっている。ただし、普通の電池のような+極の出っ張りがない。右はテスターで電圧を順次あたって、直列接続を確認しているところ。
ポアッソンの明点 武捨さんの発表
武捨さんは、光の回折を演示するのに、何かよい実験が無いかと考え、そのひとつとして三省堂のⅠBの教科書に紹介されていたポアソンの明点の実験（写真左）をやってみた。使ったものはレーザー光源、顕微鏡の接眼レンズ、4mmのスチールボール、スチールボール固定用にステンレス線とネオジム磁石。
顕微鏡の接眼レンズに通して光束を広げたレーザー光を、ステンレス線の先端につけたスチールボールにあてる。ボールの固定に磁石を使っているところがなかなかの工夫だ。位置の調節がしやすい。壁にうつったスチールボールの影をよく観察すると・・・
その影の中央に、ごく小さな明点が現れる（写真左）。例会では、光の回折の演示方法として、両刃カミソリを使う方法や、ステンレス線の影にできる回折縞（写真右）を観察する方法、単スリットの幅を（干渉縞が見えない程度に）狭めていく方法などが提案された。
また、水波や音波と異なり、光の回折はスケールが小さいことを段階的にスケールダウンしながら示すのがよいのではないか、意図的に光の干渉を見せないことよりも、干渉を伴うことを示すのがよいのではないか、といった意見も出された。
鏡文字にならない鏡 市江さんの発表
平面鏡にうつる文字がいわゆる「左右反転」の鏡文字になることはよく知られているが、大きくて柔らかいミラーシート（写真左）を用いると鏡文字でないふつうの文字を手軽に鏡にうつすことができる。黒板に大きく左右非対称な文字を書き、黒板に背を向け、鏡に黒板をうつして見る（写真右）。鏡が平面のときは、いわゆる「左右反転」の鏡像が見えるが、鏡を水平方向に軽くU字型に曲げると、黒板の文字がふつうに読める（写真下段左）。
この現象をどう解釈したらよいだろうか。一種の合わせ鏡と考えれば、左右の反転の反転でもとにもどると考えられなくもない。しかし、右の写真のような凹面鏡にうつる像も考えに入れてつじつまを合わせようとすると、それではうまく説明できないことに気づく。凹面鏡に右手を挙げた自分をうつすと左手を挙げた自分が逆さまに見える。これを水平方向のU字鏡と上下方向のU字鏡の組み合わせと考え、左右と上下が入れかわって見えていると解釈すると、平面鏡の像を左右反転していると解釈するのが不自然であることに気づく。平面鏡は左右ではなく、手前と奥、すなわち「前後反転」していると表現するのが適切である。
つまり、鏡を正面から見ることで前後が反転し、水平方向に鏡を曲げれば左右が反転、さらに上下に曲げれば上下が反転する。方向を問わず1回反転するごとにうつる文字が鏡文字になったり、普通の文字になったりする。すなわち左手系と右手系が入れかわる。ちなみに上下方向に曲げたU字鏡では、普通に読める文字が上下逆さまにうつって見える。よく考えてみれば、全く不思議なことではないのだが、断片的な知識と理解だけで、わかった気になっていたと気づかされる実験だった。
関連して・・平面鏡の実験 田代さんの発表
鏡の話のついでに、田代さんからは、中学校の理科で行う実験の紹介があった。写真のように鏡の面の前に鏡より高い筒を置く。像の上は鏡より上にはみ出るが、はみ出た筒とつながるように鏡の裏にも同じ長さの筒を慎重に置く。像の位置と一致すれば、視点を変えても像と裏に置いた筒がぴったりつながって見える。まるで透明なガラス板が間にあるようだ。像の位置は鏡に対して対象な位置だと直観的に理解できる。「鏡に映った像は、上下は逆にならないが、左右が逆になる。」とよく言われるが、実は左右も逆ではない。正しくは、手前と奥（鏡の面に対して近い遠い）が逆になるのだ。
２体問題の授業 水上さんの発表
糸で連結された２つの物体の運動に関する問題（２体問題）ではどの教科書も理由の説明なしに『軽い糸の張力は両端で等しい』と記されている。そして生徒はこれを鵜呑みにさせられ、「類題１２」(左の写真の上)の解法を覚えさせられている。試験でも正答率が低い。水上さんは、改善を目指して、授業プリントに右のような「経験値を増やそう」コーナーを導入してみた。授業手順は以下の通りである。
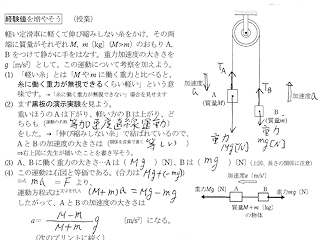
(1)『「軽い糸」とは…』は単なるつかみである。糸に働く重力を無視できない(おもりの質量が小さい)場合には低いほうのおもりが下がるのを見せた。おもりはマーカーペンのキャップを使用した。滑車は「精密滑車」を使う。（写真左）
(2)『２つのおもりは等加速度直線運動する（加速度aが生じる）』ことを実感させるために、右の写真のような黒板実験を見せる。黒板上に0，5，20，45，80㎝の位置に線を引き、質量が大きい方を0の位置に合わせてから運動開始→線の位置を通過するたびに打つ手拍子が等間隔になる。これにより、図は等加速度直線運動中の一瞬を切り取ったもの（静止状態ではない）であることがわかり、よくある誤解「Bの重力が伝わるのでTA＝mgでは？」も防げる。
(3)文中と図に「重力Mg」と「重力mg」を記入する。
(4)A＋Bを質量M＋m〔kg〕の１つの物体とみなし、これに合力Mg＋(－mg)〔N〕が作用して加速度aが生じると考えてa＝(M－m)g/(M＋m)〔m/s2〕を求める。
(5) 加速度aの向きに注目させて『張力TAは重力Mgより小、張力TBは重力mgより大』を確認してから下段左写真の図にTAとTBを記入させる。
(6)でTAを、(7)でTBを計算させる。（(4)で求めたaの値を用いる）。
(8) TA＝TBであるから共通の文字T〔N〕で表せることを確認する。続いて教科書の記述（『軽い糸の張力は両端で等しい』）を読む。
最後に、「加速度a（２か所）」→「張力T（２か所）」→「重力Mgとmg」の順で図に記入していく。授業ではこの後に「類題１２」を解かせた。水上さんは試験の正答率が上がることを期待している。
PS研公開講座報告 西村さんの発表
物理教育研究会Physics Suite研究班（PS研）の主催で8/18に東京学芸大学で行われた「物理公開講座in東京」の報告があった。当日は、都立高校を中心に30名の生徒を集めての模擬授業と、全体協議(アクティブ・ラーニング(AL)に関する新田先生の講演+グループ協議)が行われた。参加教員は89名と大盛況だった。
当日の模擬授業は、１時間目を西村さんが、２・３時間目を勝田さんが担当、それぞれPIおよびILDsの授業例として、下の写真のような課題で授業を行った。
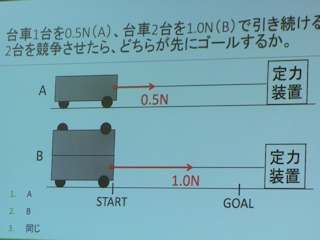
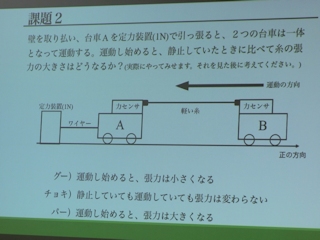
公開講座の参加教員からは「AL型授業のイメージを持つことができた」「勤務校で早速やってみたい」という声が挙がった一方で、「複数の教員で一つの科目を担当していて、共通テストや評定の問題から実施できそうにない」「ALを取り入れるだけの授業時間を確保できない」「大学入試には役立つのか」「ICT機器が揃っていないので、今回のような授業はできない」といった課題も出された。
例会では、
・教材研究、教材開発はYPCのような場に教材を持ち寄り、議論していくことが実現の近道になるだろう。
・実験器具やICT機器が揃っていなくても、実験動画を使うことで、代用できる部分もあるだろう。
・水上さんが長年作成して来られた実験動画、教材集のようなものをWeb公開すると良いのではないか。
といったコメントが寄せられた。
開発した研究者の意図を尊重し、型を守ってまずはやってみる、ということも重要だが、現場で実現するためにはどのような修正、変更、工夫が必要かといった視点も、このような講座では取り入れていかなければならないだろうと感じた。西村さんたちは神奈川県でもいずれこのような取り組みを実施したいと思っている。
この実験がうまくいく方法を教えて 車田さんの発表
車田さんから、慣性の法則の実験を生徒にやらせたいが、成功率が低いと相談があった。おもりの上下に糸をつけ、下の糸を勢いよく引くと下の糸が、ゆっくりと引くと上の糸が切れるという実験である。いろいろ事情を聞くと、おもりの質量が100gでは小さすぎるのだろうという結論になった。
「蜘蛛の糸」とpseudowork 鈴木亨さんの発表
日本物理学会誌２月号に，長崎大・後藤信行氏による，「『蜘蛛の糸』仕事をしたのはカンダタの筋力か？」という記事が「談話室」に載った。同氏は３月の物理学会年会でも同名の原著講演を行っている。芥川龍之介の短編小説に，地獄の亡者，カンダタがお釈迦さまの垂らした蜘蛛の糸を手繰って上る場面がある。このとき，カンダタの重力に逆らってカンダタに仕事をしたのは，カンダタ自身の筋力か，糸の張力かの議論があり，自身は強く張力であると主張するものである。
普通に考えると，作用点の変位はゼロなので，張力は仕事をしていない。後藤氏は，仕事の定義は「力×物体の重心の変位」であるとし，科学辞典や教科書のほとんどがそうである，と言う。実際，培風館物理学辞典や岩波理化学辞典などは「力×作用点の変位」であり，「×物体の変位」と書いているものは物体を質点扱いしている場合である。「×重心の変位」としている文献は見当たらない。
ところが，運動方程式を重心の変位で積分すると，「外力×重心の変位」が系の重心のエネルギー変化である，という関係が出てくる。この「外力×重心の変位」は “pseudowork”（ニセの仕事）と呼ばれるものである。30年ほど前，American Journal of Physics に書かれ，海外の教科書には記述されているものがあるが，日本ではあまり知られていない。
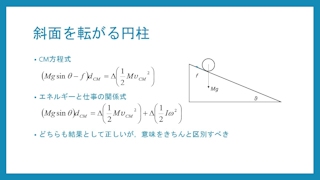
斜面を転がる円柱，階段を上る人，エンジンで加速する自動車など，束縛力は仕事をしていないが，pseudoworkは重心のエネルギー増加と等しいという例は多数あるが，本来の仕事―エネルギー関係と区別して理解する必要がある。後藤氏は外力のみが系の運動量を変化させるという事実から，「外力のみが系に仕事をする」ことを「自明」としてしまった，「自明性の罠」に陥ったものと思われる。
鈴木さんの発表資料（ＰＤＦファイル174KB）はここ。
二次会永山駅前「塚田農場 京王永山店」にて
15人が参加してカンパーイ！。今日の例会は、発表数こそ少なかったが、内容の濃い、考えさせられる話題が多かった。実験や授業のやり方について、落ち着いて突っ込んだ議論ができることはよいことだ。若手の参加者にも大いに参考になることだろう。
ＹＰＣホームページへ｜ 天神のページへ｜ 他のサークル・団体等へのリンク｜ 次回例会のご案内
