2005.12.10（土）　　『錐体鏡を使った多面体創作』　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　河崎　哲嗣，南　　隼矢

今年度１３回シリーズの公開講座。恥ずかしながら私で〆とさせて頂きました。
後期シリーズの序盤は、確率等などの小学校で扱われない分野、中盤は、数を中心にした内容。
そして終盤は、図形を扱う幾何分野に纏めました。さすがにクリスマス前の1年間の決算でしたので、
参加者をガッカリさせずに喜んで帰ってもらおうと思案しました。

講師は私です。初めてのＨＰ上の自分の姿。 見苦しいことに今更気づきました。	平面と空間の敷き詰め の問題	立方体の2分割、3分割

上記のことがらは、後に登場することがらの導入です。平行四辺形→菱形、長方形→正方形、立方体の大きさ（体積）の比較
四角錐の大きさの問題を参加者に模型（展開図は持って帰ってもらいました。）を示しながら、公式の由来について
少し解説しました。
大人も楽しんでもらおうと、多面体に関する英文の文献や書籍の内容を紹介しました。

前回の小波先生の講義の続きとして、ケプラーの 星形多面体の紹介。	「MOL-ＴＡＬＯ」を用いて、ダイヤモンド構造を見る視点を変え ると三角形、四角形、六角形が見える。「物事」の思考も同様	運搬中に壊れたのですが、参加者から「作りたい」という声があがった正多面体の入れ子構造。

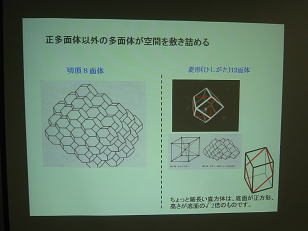
何故立方体の分割を考えさせたかは、ここに繋が ります。準正多面体・双対多面体の話。	できたものを比較して 感動の声があがり、ホッ	私の過去に作った紋様のついた色々な模型を肌で触って実感を得てもらいました。（休憩タイム）

後半！

鏡の世界に入る前にＳＦ小説作家の星新一氏の「鏡」を参加者で朗読し、三面鏡で遊んだ頃の不思議な気分を味わいました。
（子供達への読書の勧め）

　平面の敷き詰めと空間の敷き詰めをリンクさせる道具としての「鏡」です。

正四面体の錐体鏡を作りました。中を覗くと	光が反射して見にくいですが、正２０面体ですね。 ここで何故入れ子構造を紹介したかを理解して もらったわけです。

算数・数学を中心にしながら、文化や生活、歴史、他の科学分野、人間性とTotal的にバランスを備えてもらおうと

盛り沢山に話しをさせて頂きました。喜んで帰ってもらったかな？夢を抱いてくれたかな？　　　　了




授業で使用したものですが、全て網羅・掲載しておりません。ｱｼｶﾗｽﾞ

すべてＰＤＦファィルです。
使用プリント（画像取り込みサイトや参考文献も記載しました。営利目的に使用しないでください。）
パワーポイント（授業で使用したもの）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

【各立体の展開図】
四角錐（展開図らしくありませんが、許してください。立方体の１／３体積です。）　　　　　　　　　　　
切頂八面体と菱形１２面体の展開図（パーツは立方体の１／２と直方体の１／２の立体です）　
　※(失敗談)のりしろを余分に作ってしまいました。

【使用文献】：星新一「鏡」（新潮文庫「ぼっこちゃん」にあります。御購入ください）
【英文資料】：多面体の歴史〜現在　　（英国の子ども向けパズルだったと思います。）