湘南台高校・山本明利
ドップラー効果の式といえば、ほとんどの教科書や参考書が判で押したように
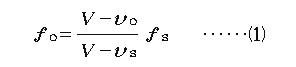
という公式を掲げています。もちろんここにVは音速、添字Oは観測者、Sは音 源を意味し、vはそれぞれの速度、fは振動数です。蛇足ながら、本によっては SからOに向かう向きを正にとれなどと指示してあるものを見かけますが、これ は邪道で、音速も含めてすべての速度を同じ座標軸のもとで符合付きで表せば、 この式はあらゆるの場合を尽くしています。 ところで、生徒はよく(1)を丸暗記しようとして分子分母を取り違えるので、 私は意識的に次のように書き替えて授業をしています。
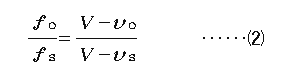
この形ですと、対称性がよいので記憶しやすく、仮に「OはONGENだったかな?」 などと上下を取り違えても正解が得られますので試験対策としては有効です。で も「試験のための物理」ではちょっと悲しいので、もう少し掘り下げてみること にします。式(2)をさらに変形して、
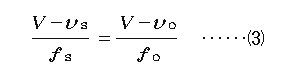
としてみると新しい視点が見えてきます。V−vは音源や観測者に対する音の相 対速度(相対音速)を意味しますから、式(3)は言葉で書けば、

ということで、波の基本式V=fλを思い起こせば、上式は「音源から見ても観 測者から見ても波長は同じである。」と述べていることになります。 つまり、音源から見ると音波は1秒間にV−vSの距離を進みますが、その間 にfS個の波が発せられるので、音源からはV−vS/fSという波長の波が進 んでいくのが見え、一方の観測者は1秒間にV−vOという長さの内に含まれる fO個の波を受け取るので、観測者から見るとV−vO/fOという波長の波が やって来るように見えるわけですが、相対論的効果を考えなければ、運動してい ても長さの変化はないので、この波長は両者にとっての不変量でなければならな いわけです。 言うまでもなくドップラー効果は「波源や観測者の運動の結果、観測者が観測 する波の振動数が波源が発するそれと差を生じる現象」なのですが、これを波源 →観測者という座標系の乗りかえ(ガリレイ変換)に伴う物理量の変化と考え、 この変換の中では「長さ」すなわち「波長」は不変量だという視点に立って式(3) を導くのもすっきりしていていいかなと思います。すなわち、 「波長は波源、観測者の両者にとって共通なので、それぞれの立場でλ=V/f を求めて等しいと置けば式(3)を得る。」 証明はこれだけでいいんですね。
【YPCニュースNo.107に掲載】 (PDF版176KB)