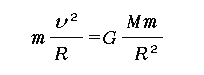
学生読み物:人工天体の運動学 (PDF版1179KB)
山本明利
1.宇宙速度 2.人工天体の速さ 3.ホーマン軌道 4.スイングバイ航法 5.スイングバイ・最近の実例
人工衛星や惑星探査機の「飛び方」について、高校の教科書程度の力学知識で理解できるような解説をしてみます。ちょっといっしょに考えてみませんか。
地球を回る人工衛星の対地速度から考えましょう。これは高等学校・物理Ⅱの円運動の単元で必ず登場する教材です。円運動の運動方程式は
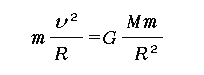
となります。ここにRは地球の中心からはかった人工衛星の軌道半径で、mは衛星の質量、Mは地球の質量です。右辺は地球が衛星を引く万有引力(重力)の大きさになります。これをvについて解くと
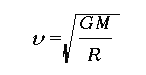
が得られます。
万有引力定数 G=6.67×10-11[Nm2/kg2]、 地球の質量 M=5.97×1024[kg]
を上式に代入すると、
| 地表すれすれに回る人工衛星 | R=6.4×106[m] | v=7.9[km/s](第一宇宙速度) |
| 静止衛星 | R=4.2×107[m] | v=3.1[km/s] |
| 月(地球の天然衛星) | R=3.8×108[m] | v=1.0[km/s] |
となります。軌道半径の平方根に反比例して遅くなるわけです。あくまで地球を固定して考えた対地速度だという点に注意してください。
さて、地球は太陽の周りを公転していますので、月や人工衛星を従えて宇宙空間を突っ走っています。その速さも上記の公式で求まります。今度は地球の質量ではなく
太陽の質量 M=1.99×1030[kg]
を代わりに用いるだけです。Rは惑星の公転軌道半径です。地球の場合は
R=1.5×1011[m] より v=30[km/s]
となります。各惑星についてこれを計算することができますが、ちょっとさぼって理科年表から答えを引用しますと次ページの表のようになっています。「天文単位」は太陽-地球間の平均距離で、すぐ上に書いたRの値のことです。
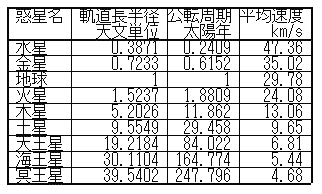
太陽から遠い惑星ほどゆっくり動いていることになりますね。足の遅い人が外側のトラックを回っているんですから公転周期には著しい差がついてきます。
次に、脱出速度です。脱出速度とはその天体の引力を振り切って二度と戻らないための初速度ですが、こちらは力学的エネルギー保存の法則
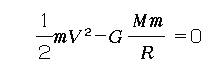
から
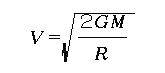
と求まります。前の公式とよく似ていますが、ルート2倍になっています。Mは親天体の質量、Rは出発点の位置で、親天体の中心から測ります。地球の質量と地球の半径を入れると、V=11.2[km/s]となります。いわゆる「第二宇宙速度」です。これも対地速度であることに注意してください。惑星探査機は一応この速度を越える初速度で地球を飛び立つことになります。一応と書いたのは、最近では裏技が開発されているからですが、それについてはあとで触れることにしましょう。
ちなみに、初の金星探査機マリナ-2号(1962年打ち上げ)は対地速度11.5 [km/s]、初の木星探査機となったパイオニア10号(1972年打ち上げ)は対地速度14.5[km/s]で地球を離れています。
火星や木星などの外惑星を探査するためには、太陽系内で地球の位置より高い位置エネルギーの所に上げてやる必要があるわけですが、そのためには上表の地球の公転速度よりも速い速度を与えてやらなければなりません。この場合の速度は太陽系に対する速度ですので、打ち上げ時の対地速度を地球の公転速度に合成したものを考えます。早い話が29.8+11.2=41.0[km/s]とすれば無駄がないので、ロケットは地球の進行方向にむかって打ち出せばよいわけです。ついでに地球の自転による地表の速さ(緯度によって異なるが数百[m/s]の程度)も利用してしまえというわけで、発射地点の自転運動の向きが公転運動と同じになる時に打ち上げればさらにお得です。それは発射地点が太陽と反対側に来るときですから、外惑星探査機の打ち上げは大抵深夜になるのです。
金星などの内惑星を探査するときはこの逆で、地球の公転速度より遅くしなければなりませんんから、真っ昼間に東向きに打ち上げます。すると、打ち上げ速度と自転の速さが地球の公転速度から差し引かれて、探査機は太陽系の内側に向かって「落ちて」いくことになります。ですから上記のマリナ-2号とパイオニア10号は打ち上げ時刻がまるで違っていたはずです。
さて、脱出速度の話のついでに、太陽系からの脱出速度にも触れておきましょう。太陽からの引力を振り切って、太陽系の外へ飛び出すための初速度です。上の脱出速度の公式に、Mとして太陽質量、Rとして出発点の惑星の軌道半径を入れます。地球の場合は42.1[km/s]となります。実は上の各惑星の平均速度のルート2倍です。これから地球の公転速度を差し引くと12.3[km/s]となります。さらに地球の引力を振り切る分も上乗せすると16.7[km/s]の対地速度が必要で、これを「第三宇宙速度」と呼んでいます。
さて、人工天体は主に経済的な理由から、軌道の変更の際にほんの短時間推力を使用するほかは、その飛行の大部分を慣性飛行ですごすわけで、天体からの万有引力に身を任せて運動しています。その意味では天然の天体と何ら区別はありません。親天体が一つなら単純な楕円運動を行なうだけです。その速度は力学法則に従って決まります。言い換えればケプラーの法則を満たさなければなりません。好きなところを好きな速度で飛ぶというわけにはいかないのです。
そういう意味で、スピードで宇宙船の性能を比較するのは全く無意味です。アポロ宇宙船は地球を出発するときには、スペースシャトルよりずっと速かったでしょうが、月の手前では1[km/s]程度の速さに落ちていたはずですし、月周回軌道上では1.7[km/s]の速さで回らなければならなかったはずです。
話が脱線しますが、天然の天体で一番速くなるのは何かというと、これは文句なしに彗星(ほうき星)です。これとてケプラー運動ですから太陽から遠いところではうんと遅いのですが、太陽に近い所に近日点を持つ彗星は近日点近くでは猛烈な速さになります。まさに「彗星のように現れて、彗星のように去っていく」のです。なにしろ冥王星の外側から太陽めがけてまっしぐらに「落ちて」くるわけですから。仮に無限遠からやってきて太陽表面をかすめるとすると、その速度は太陽からの脱出速度に等しくなります。前に示した公式
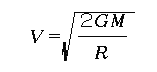
に太陽質量と太陽半径を代入すると、実に600[km/s]を越す速度になるのです。そんな彗星が実在するからおどろきです。太陽をかすめる彗星群として有名な「クロイツ群」という彗星のグループがそれです。中でも1965年に発見されたイケヤ・セキ彗星は見事な尾を伸ばして当時話題になりました。クロイツ群の彗星の中には太陽に飛び込んで「昇天」してしまったものもあります。
人工衛星や人工惑星を目的の軌道に投入する基本技術は軌道移行、つまりある軌道から他の軌道に乗り移ることです。ロケットの推力により必要な方向に必要な増速を行なうことでこれを実現します。それは多すぎても少なすぎてもいけません。現在の軌道と、移行先の軌道とで厳密に決められてしまいます。
最もスタンダードな方法は「ホーマン型移行」と呼ばれるもので、ある円軌道から、遷移軌道(ホーマン軌道)と呼ばれる楕円軌道を経て他の円軌道に乗り移るやり方です。典型的な例が静止衛星の軌道投入です。
静止衛星(気象衛星や放送衛星など)を赤道上空36000kmの円軌道に上げるときは、まず地表すれすれの円(に近い)軌道から接線方向に加速して地球を回る楕円軌道に乗り移ります。このとき楕円の地球から一番遠い点(遠地点)がちょうど目標の静止軌道に接するように計算して噴射を行ないます。次に、衛星がちょうどこの遠地点にきたときにやはり接線方向に増速を行ないます。遠地点(アポジapogee)で行なうので、この噴射をアポジキックなどいい、そのために搭載していくロケットエンジンをアポジモーターなどと呼んでいます。適切なアポジキックを行なえば、めでたく目的の静止軌道に入れます。あとは微修正をするだけです。こうした軌道移行をしくじって宇宙の粗大ゴミになってしまう衛星もあります。
惑星探査機でも基本的には同じ方法を用いることができます。事実、初期の金星や火星の探査機はホーマン軌道を通って目的地へ向かいました。
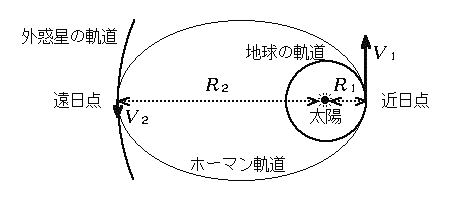
地球軌道(半径R1)を出発して、外惑星の軌道(半径R2)へ向かう場合を考えましょう。ホーマン軌道の近日点(地球軌道との接点)における速度V1と、遠日点(外惑星軌道との接点)における速度V2は力学的エネルギー保存の法則と角運動量保存の法則(面積速度一定の法則)を満たさなければならないので、
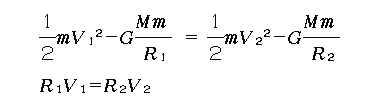
が成り立ちますから、これを解いて
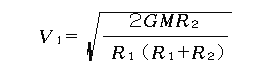
が得られます。例えば地球から木星に行く場合だと、木星の軌道半径は5.2天文単位であることからこの速度は38.6[km/s]と決まります。地球軌道近傍で接線方向にこの速度を与えてやれば探査機はとりあえず木星軌道に達します。もちろん到着したときそこに木星がいないとだめですから、打ち上げの時期は限られます。上記の速度は地球の公転・自転の速度も利用すれば比較的簡単に実現できます。ただし、ここでは地球の引力圏を脱出するエネルギーについては考慮していません。引力圏を脱したところで上記の速度にならなければなりませんが、深入りはやめます。
ところで、このホーマン型移行の欠点は何かというと、時間がかかることなのです。ケプラーの第三法則によると軌道長半径の3乗と公転周期Tの2乗が比例しますので、ホーマン軌道の片道の時間T/2はすぐ計算できます。単位を天文単位と太陽年で表すと比例定数は1になりますから上記の関係は
![]()
と書けます。地球から出発する場合はR1=1です。T/2を求めると木星の場合で2.7年、海王星まででかけると実に31年の歳月を必要とすることがわかります。外惑星探査ではこの方法は現実的ではありません。
パイオニア10号は1.8年、11号は1.6年で木星に達しました。ボイジャー2号は1.9年で木星に達しました。共にホーマン軌道はとらなかったわけです。それは木星より先に目標があったからです。木星は通過点の一つに過ぎなかったのです。
ボイジャー2号は地球を出発してから12年で海王星に達しました。ずいぶん行程を短縮していますね。その秘密が有名なスイングバイです。
さて、いよいよスイングバイ航法の話に入りましょう。高校教科書レベルの解説をめざします。
スイングバイ(フライバイともいう)は、天体の運動とその重力を利用して推力を使わずに人工天体を増速(または減速)する経済航法で、燃料および経費の節約と航行期間の短縮という一挙両得をもたらす、惑星探査には欠かせない技術です。利用する天体の動きに合わせた精密な軌道制御を必要としますので、技術的には高級になります。いつ頃から実用化されたものか私もよく知りませんが、これをあざやかに演じてNASAの技術を世に示したのは1973年に打ち上げられて、木星・土星を探査したパイオニア11号だったと思います。そのちょっと前に初めて木星を訪れたパイオニア10号も、土星には行きませんでしたが、木星を観測後太陽系の外に出ていますので、ここでリハーサルが行われていると思います。きっとそれ以前にも実験は行われていたのでしょう。その後さらに華々しい活躍をしたボイジャーが有名になりましたが、その陰には地道な技術の積み上げがあったのです。
スイングバイの原理は、力学的エネルギー保存の法則と、運動量保存の法則が共に成り立つと考えれば説明することができます。運動量とは運動物体の質量mと速度vの積mvで定義される量で、物体系全体で運動量のベクトル和が一定に保たれるというのが運動量保存の法則です。簡単のため、少々無理をして直線上の運動で考えてみましょう。
本論に入る前に、はじめ十分離れていた2物体が万有引力のみで相互作用しながら互いに近づき、最接近後再び離れていくという運動は、一種の「衝突」であという事実を確認していただきたいと思います。二つの物体は接触しませんが、ずっと遠くから見ると二物体は互いにぶつかって跳ね返るように見えます。「重力衝突」などと呼ぶこともあります。例えば太陽系の辺縁からやってきた彗星が太陽をかすめて再びもと来た方向へ飛び去る運動は、地球軌道など見えないぐらい遠くから観察すれば、太陽に当たって跳ね返るように見えるでしょう。
エネルギー保存と運動量保存の2法則が共に成り立つ衝突では、相対速度(一方から見た他方のみかけの速度)の大きさは、衝突の前後で等しくなります(向きは反対)。いわゆる「完全弾性衝突」です。証明は省きますが、力学のよい例題になります。天体から見ると、探査機は最接近後、近づいてきたときと同じ速さで遠ざかっていくように見えます。
ところで、天体は動いています。仮に天体の軌道上の速度をVとしましょう。その正面の十分離れたところから探査機が速度-vで逆向きに運動してくるものとします。相対速度の大きさはv+Vです。接近時には万有引力がはたらき互いの運動を変化させますが、天体と探査機ではどだい勝負になりませんから事実上天体はびくともせずにVという速度を維持し、探査機はその周りをくるりと回ってもと来た方向に引き返していきます。天体から見た相対速度の大きさは十分離れたときには同じv+Vになっていなければなければなりません。ということは、探査機の速さはv+2Vになったということです。速さを比べるといつの間にか2Vだけ増えています。ちっとも推力など使っていないのに・・・不思議ですね。
厳密な計算をすると、天体と探査機の質量をM、m、はじめの速度をV、v(上とvの符号のとり方を変えましたので注意してください)、最接近後再び十分離れたときの速度をV’、v’とすると、
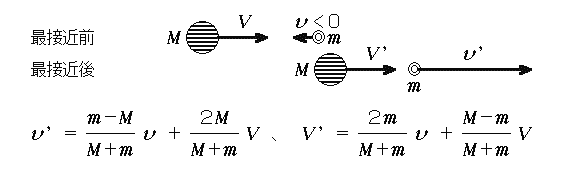
という結果を得ます。実は天体の速度もほんのちょっぴり変化しているのです。M→∞とすると、v’=-v+2V、 V’=V となって前述の考察に一致します。ですから、探査機は天体の運動量と運動エネルギーをほんの少しかすめとって速さを増したことになるのです。その分天体はわずかに遅くなっているわけです。でも、Mとmの比を考えたら、「月や惑星の軌道が変化するのでは?」などという心配は無用であることがわかると思います。
上の考察で、天体の正面から探査機が近づくという想定を不自然に感じられた方も多いと思います。実際の運動は平面運動として捉えなければなりませんが、その場合は天体の速度に直角な探査機の速度成分は、十分離れれば変化がないと考えてください。天体の速度と同じ方向についてのみ上の考えを適用します。探査機の軌道は最接近時を境に「く」の字型に折れ曲がります。
5.スイングバイ・最近の実例
わが国の宇宙科学研究所研が誇る工学試験衛星「ひてん」は1990年1月24日に打ち上げられ、大活躍をしました。残念ながらマスコミではあまり報道されなかったのですが・・・。彼の偉大な業績は
●月を利用して何度もスイングバイを行ない、軌道変更の実験をした。
●月周回軌道にわが国初の孫衛星「はごろも」を投入することに成功。
●地球大気によるエアロブレーキ実験
●ラグランジュポイントを利用した高度な軌道操作できわめて経済的に自身を月周回軌道に投入。
●わが国初の月面「硬着陸」、つまり衝突。(1993年4月11日)
などでした。これは世界的にも高く評価されており、高度な軌道制御技術の確立に貢献しました。もっともっと華々しく報道されてしかるべき成果でした。マスコミの無理解が悲しいです。なお、同じ宇宙研の磁気圏観測衛星「ジオテイル」も月スイングバイを積極的に活用して広範囲に地球磁気圏の観測を行ないました。
パラボラアンテナが開かなくてたいそう不自由な観測を続けているアメリカの木星探査機「ガリレオ」は、1989年10月に満を持してスペースシャトルから打ち出されましたが、木星に行くはずなのになんとブレーキをかけて地球軌道の内側へと「落ちて」いきました。金星に近づいてスイングバイをするためです。90年2月金星でスイングバイ、返す刀で90年12月今度は地球でスイングバイしましたがまだエネルギーが足りず、火星と木星の間にある小惑星帯までで引き返してきて92年12月、もう一度地球をかすめてスイングバイ。これでやっと木星まで届いて95年12月目的地に到着しました。実に気の長い旅です。もちろん計画どおりの軌道なのですが、財政上の理由と技術的な事情とがさまざまにからんでこういうことになりました。すべては完璧に運んだのですが、アンテナが・・・
ガリレオ君は今も元気で活躍中です。ちょっと声が遠い以外は順調です。
NIFTY-SERVE【理科の部屋】への書き込み(96/12/14-17)より (PDF版1179KB)