

2006年7月8日(土)愛知工業高校での例会の記録です。
| 7月5日の未明に、北朝鮮がミサイルを数発発射しました。日本や韓国の新聞やテレビは大騒ぎでした。 正確に目標を捕らえてミサイルを飛ばす技術があれば、それを民生用に生かして産業を興隆させることも可能なのに・・・、と思わずにいられません。 科学技術が軍事中心に使われるような社会は、皆が不幸になる社会だといえるでしょう。全ての人々に幸いをもたらす科学を次世代に伝えたいと、強く感じます。 |
| 電子波のビデオ紹介 (林さん) 日立製作所フェロー外村彰さんの研究を説明する「電子波で見るミクロの世界」の紹介です。 電子顕微鏡内で電子を1個ずつ 飛ばし、到着点を検出器で調べます。 1つづつ到着点の記録が増えていきます。最初はランダムだった点列が、数が増えるにしたがって写真のような縞模様を作ります。 量子力学の波動関数の意味を目で見える形にした優れた研究です。 |
 |
 |
| 静電高圧ゼネコン (奥谷さん) 中村理科の静電高圧ゼネコンです。¥13,800です。 ハンドルを回転させるだけで、手軽に高電圧を作り出せます。 手作りライデン瓶にためると、5mmぐらいの放電が得られます。 |
 |
 |
 |
 |
 |
| 残念ながら放電の瞬間は撮れなかった・・・・・ | 上は手作りの高圧発生器。塩ビパイプと猫皮の摩擦により電気を発生させます。ハンドルを回し てやるとどんどん電気がたまります。 | |
| フリーピストンスターリングエンジン (奥谷さん) jaxa(宇宙航空研究開発機構)の研究を元に作られたスターリングエンジンの紹介です。 エンジンをお湯を入れたコップの上に置くと、中央部のピストンが振動します。 動く仕組みを理解するには時間がかかりそう・・・・・ <参考> http://www.f-plan.co.jp/other-energy/ stirling-engine-cp.html |
 |
 |
 |
 右端の円形金属内に十字形のシートがあり、これがスプリングの役目を果たし、中央のスポンジを跳ね上げるようです。 |
| 立体スペクトル (伊藤 政夫さん) 光が立体的にスペクトルに分かれている様子を見せられないかと思い、OHPを使って工夫しました。 OHPの投射面に四角い細長い穴のあいた紙を置き、鏡の前にグレーチングシートをおきます。 |
 |
 鏡の前にグレーチングシートをおきます。↑ |
| 部屋を暗くすると、回折光がはっきり見えます。(中心に近い方が青色になりますね) スクリーンを横に動かすと暗いですが2次の回折光が見えます。 |
 |
 |
| この光を、線香の煙を充満させた容器に入れると・・・ 何と確かに回折光が立体に見えます。 |
 |
 |
| さらに、この立体スペクトルを横から見ると白く見えます。3原色の重なりで白く見えるようです。 0次の白色光はちゃんと遮光した状態での写真です。 グレーチングシートに変えてプリズムを置くことでも同様な立体スペクトルを得られます。 面白いですね。 |
 立体スペクトルを横から見ると・・・ |
 グレーチングシートの代わりにプリズムを置く。 |
四角の穴の半分に赤色の透明下敷きを置くと 回折光が下のようになります。赤い色の下敷きは青や緑の光を吸収することがわかります。   |
四角の穴の半分に青色の透明下敷きを置くと 回折光が下のようになります。青い色の下敷きは赤の光を吸収することがわかります。   |
| 色の問題 (飯田さん) ここに赤、緑、青の色紙があります。 黄色のセロファンを通してみると、黒っぽく見えるのは何色の紙でしょう。 予想 ア 赤の色紙 イ 緑の色紙 ウ 青の色紙 皆さんわかりますか。 同様に赤や緑のセロファンを通してみると、どう見えるか予想してみてください。 ↓ |
 |
|
   |
||
| 以前の例会に「新光の三原色装置」を発表しましたが、今度はその大型版。 ハロゲンライトにゼラチンフィルターをつけ3原色を得ています。 3色の重なり部分は白色になりますが、残念ながらやや色づいて写っています。 棒を置くと、影が色づいて見えます。 |
 |
 3色の光をスクリーンにあてます。 |
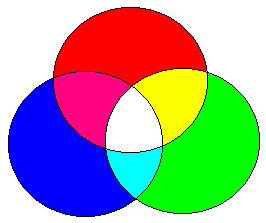
| 白色になる所に棒を置くと、影が色づいて見えます。 影の方向により色が異なります。 頭を置くといろいろな色の影ができます。 色のベン図を参考にお考えください。 |
 |
 |
| 光源に使ったハロゲンライトは線光源として優れており、値段も安く(¥1000程度)フィルターの色を選べば、色の実験に役立ちます。 発熱が大きいのが問題といえますが・・・・ |
 |
 |
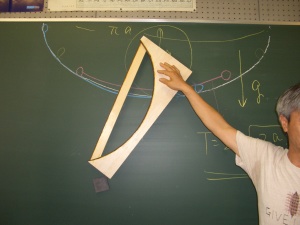
| サイクロイド曲線と 最速降下線 (川田さん) 定直線に沿って円が動いたとき、円周上の定点の軌跡をサイクロイドといいますね。生徒が数学でこれを習っても、その意味を理解する機会がないということで、教材を作りました。 サイクロイド曲線と直線で小球をころがすと、サイクロイド曲線の方がかなり早く着きます。 サイクロイドは最速降下線なのですね。 |
 |
 |
 |
 |
|
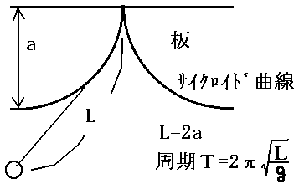
| <参考> 最速降下線問題 1696年、ベルヌーイが次のような問題を提起した。 「質点がある点 A からスタートして重力のみを受けて滑らかな斜面を転がり落ちるとき、最短時間で別の点 B まで辿り着くには斜面をどのような曲線にしたら良いだろうか。」 ベルヌーイ自身もニュートン、ライプニッツ等が解いたといわれる有名な問題です。 |
||
| この教材を傾けたらどうか。という質問が出ました。 サイクロイドはパイプにすると考えます。(小球が落ちてしまいますから・・・) 直線部分が真下を向けば自由落下ですから、これより速くなることはないですね。するとある角度で両方が同じになる角度がありそうですね。 解析的に解くと・・・・・・難しそう・・・・・ |
 |
|
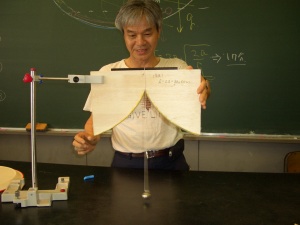
| 続いてサイクロイド振り子です。 単振り子の周期は振幅が小さいという前提で一定ですが、現実には振幅が大きいと周期は大きくなります。 このサイクロイド振り子は厳密に振幅によらず周期が一定です。 サイクロイド曲線にそって小球を転がしても周期一定の振動をします。 |
 |
 |
 |
||
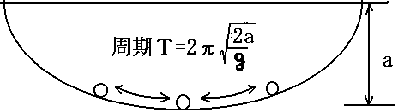 |
||