大きなダイオードがいくつかあったので、外装を削ってみました。
写真ではよくわかりませんが、中身は金属が接続されているだけのように見えます。
半導体の特徴や働きは、外見からはうかがえませんね。
2010年9月25日の例会の記録の第2ページです
| ダイオードの中身 (前田さん) |
| 大きなダイオードがいくつかあったので、外装を削ってみました。 写真ではよくわかりませんが、中身は金属が接続されているだけのように見えます。 半導体の特徴や働きは、外見からはうかがえませんね。 |
|
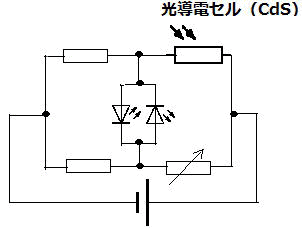
| 暗くなると点灯する仕組 (前田さん) |
| 暗くなると点灯する街灯がありますが、ホイートストンブリッジ回路で、この仕組みを理解するための回路を作りました。 右図のような回路で、CdSを覆うと、LEDが光ります。どちらのLEDが光るかで、電流の向きもわかります。 |
 |
 |
 |
| ダイオードの性質 (前田さん) |
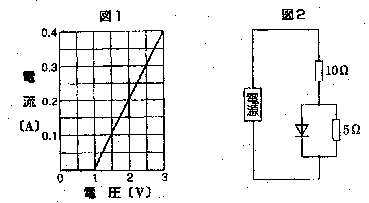
| 【問題】 図1のような特性をもつダイオードを、図2のように接続し、.電源電圧を変えていった。 (1)ダイオードにかかる電圧が0.5Vのとき、電源電圧は何Vか。 (2)ダイオードに電流が流れるのは、電源電圧が何V以上のときか。 (3)電源電圧が8Vのとき、ダイオードの電流は何Aか。 このような問題演習をしますが、計算のみより実物のほうがより理解が深まるだろうと思い、実物モデルを作りました。 |
 |
|
  |
||
ダイオードの代わりに発光ダイオードを使って、電流を見えるようにしました。 可変電圧の電源を使い電流計と電圧計で値を確認します。 問題文の抵抗の値と実物の抵抗の値が異なるのは、LEDは流せる電流の値が小さく、問題文のような大きな電流は流せないからです。 |
||
| LEDと整流ダイオードの性質の違いも、簡単な回路で示します。 整流ダイオードは豆球を点灯させるだけの電流が流せますが。LEDは豆球を点灯させるだけの電流を流せません。(自分は光っていますが・・・・) |
 |
 |
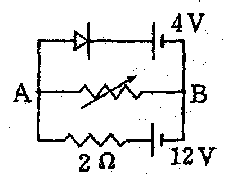
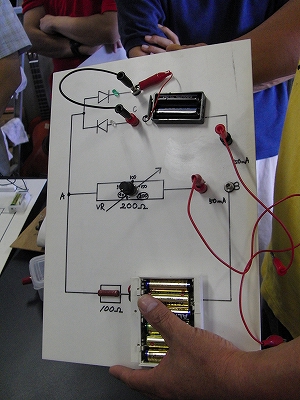
| 次の問題です。 【問題】 理想的なダイオードをもつ図の回路で可変抵抗を次の値にしたときAB間を流れる電流はいくらか。 (1) 0.5Ω (2)2Ω 電流の向きを見られるように、LEDを2つ反対向きにつけてあります。(これも実物は問題文の抵抗値を調整してあります) 中央の可変抵抗を回すと片方のLEDが点灯したり消えたりします。 |
 |
 |
| 最近見かけないセンターゼロの電流計です。これを使うと、電流値が+−に変化しても、電流計の接続をそのままに測定できます。(教育用電流計はこの方が良いのではと思えます) 残念ながら(?)理想的なダイオードはありませんのでこのときの電流値を測っても計算どおりにならないでしょう・・・・。 |
 |
 |
| 最後です。 【問題】 内部抵抗力撫視できる2つの電池、いくつかの抵抗、ダイオードD、スイッチSを用いて図のような回路をつくった。Rは可変抵抗で、DはA→Bの向きには抵抗0で電流を流すが、逆向きには電流を通さない。はじめSは開かれている。 (1) R=0[Ω]としたとき、Dには電流が流れなかった。その理由を15字程度で述べよ。 (2) Rを0[Ω]からしだいに大きくしていくと、やがてDに電流が流れるようになる。このときのRの値はいくらか。 (3) R=60[Ω]としたとき、Dを流れる電流はいくらか。 (4) 次にSを閉じる。Rを0[Ω]からしだいに大きくしていくと、やがてDに電流が流れるようになる。このときのRの値はいくらか。 |
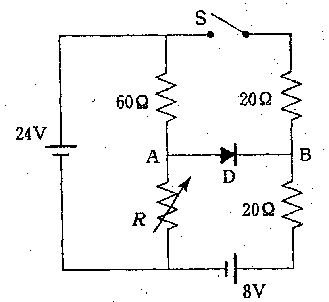 |
|
 |
これも、電流の向きを見られるように、LEDを2つ反対向きにつけてあります。 可変抵抗をまわすと、光るLEDが変わります。 |
 |
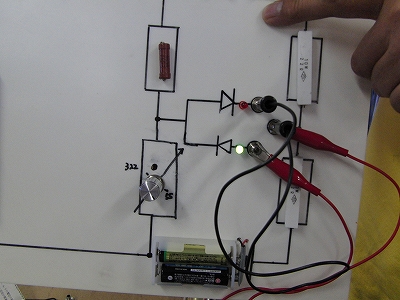 |
実物を使って、生徒に回路の計算の意味をより深く理解させようとしたわけですが、何より自分が一番勉強になったとのことです。 |
|
| 衛星「みちびき」の軌道 (杉本さん) |
| 9月11日に、準天頂衛星初号機「みちびき」が打ち上げられました。みちびきはGPS補完・補強のための技術実証・利用実証を目的としています。 この衛星は軌道周期23時間56分で、恒星に対する地球自転と同じです。つまり赤道上空であれば静止衛星となりますが(地球中心から見ると赤道上の1点に静止している)、実際は地球中心から見ると、地上に右のような8の字模様の軌跡を描きます。 みちびきの軌道はどんな軌道なのでしょう? いきなり楕円軌道では難しいので、地球自転と同じ等速円運動だとどんな軌跡になるか考えます。 単振動する南北の直線を描くように思えますが違います。 |
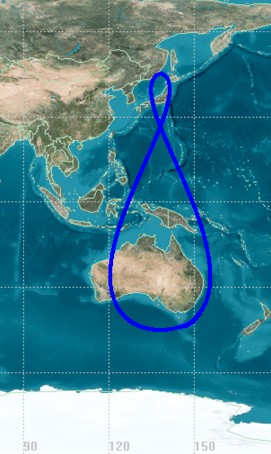 wikipediaから参照 |
|
 |
 |
軌道が傾いていると、等速円運動をしていても、地上から見ると緯度により経度に対する速度が異なります。そのため緯度により進んだり遅れたりすることになるので、赤道に中心を持つ8の字になります。 実際のみちびきは図のような上が小さい8の字です。これは、みちびきの軌道が楕円軌道であることを示しています。 ではここで問題。 楕円軌道だと、近日点と遠日点がありますが、日本上空ではどちらの点になっているでしょう。 ケプラーの第2法則とみちびきの目的を考えれば答がでますね。 <参考> http://www.satnavi.jaxa.jp/project/qzss/movie/index.html |
|
| ベルヌーイの定理による揚力実験の変化 (近澤さん) |
 パイプとドライヤー。 |
 電球が点灯した状態で浮いています。 |
ベルヌーイの定理の意味するところは、流体の流速が上がれば圧力が下がる、といえます。このため物体の両側で空気の流れの速度が異なれば、物体は力を受けることになります。 この現象を示す方法の変遷について話してくれました。 最初は、パイプと発泡スチロール球。パイプを吹いて、球を浮かせます。 次に、ドライヤー。ピンポンだまを浮かせられます。 流速があれば、電球も浮かせられます。(ブロワーで風を送っています) 最後に、大型バルーン。 ブロワーで膨らませ、ブロワーで風を送りバルーンを浮かせます。大きいと迫力がありますね。 |
|
 |
 |
| 自作シグナルジェネレーターと表示装置の利用応用例 (田中さん・船橋さん) |
| 自作シグナルジェネレーターと表示装置の利用応用例を見せてくれました。 (1) 振動数の測定。 コンデンサーマイクの信号をカウントして、0.2秒間の測定で振動の周期を正確に測って振動数を出しています。 |
 |
 音さの表示は370Hz。 良い測定値が出ています。 |
| (2) 回転数の測定。 フォトダイオードへの信号が羽の動きで切られることをカウントして回転数を測っています。 太陽電池モーターがどのくらいの速さで回転しているか、あまり気にしていないと思いますが、電池でまわした場合の実測値で40回転/s程度でした。 |
 |
 |
  |
||
| LEDストロボで同じ振動数の光を当てると、羽が止まって見えます。感動ですね。 |
||
(3) ドップラー効果 鉄道模型の電車に超音波スピーカーをつけて動かします。 超音波マイクで音を拾い振動数を測定します。マイクに近づくときと遠ざかるときで振動数が異なります。 |
 |
 |
 |
 |
| 電車が近づくときの振動数。静止時は40000Hz。 | 電車が遠ざかるときの振動数。 |
ドップラー効果の式で計算すると、電車の速度は0.50m/sとなります。 ビースピーでこの電車の速度を測ってみると、0.44m/s。まあまあの一致といえそうです。 電車に反射板をつけて、自動車のネズミ捕りの仕組みをしてみたら、という声も出ました。 <参考> 自作シグナルジェネレーター (田中さん) 新型LEDストロボ (田中さん) |
|