　

　２０１３年９月２８日（土）愛知工業高校での例会の記録です。

　今年のノーベル物理学賞は、力を伝える粒子に質量を与えるメカニズム「ヒッグス機構」の理論を提唱したベルギー・ブリュッセル自由大学名誉教授のアングレール博士と英エディンバラ大学名誉教授のヒッグス博士に授与されることになりました。理論が提唱されたのは1964年。半世紀の時を経て、昨年、スイスのＣＥＲＮにある世界最強の加速器LHCで、ヒッグス粒子とみられる新粒子が発見されたことが、今回の受賞につながりました。実験を行った人たちにも賞をあたえるべきだという意見もあったようですが、長い時を経て、理論が証明されたことに浪漫を感じずにはいられません。

　物理サークルの活動も、まもなく５０年になろうとしています。私たちの活動はそれほど陽の目を見るものではありませんが、志は高く、日本の科学の発展のために貢献すべく、地道に細々と続けていきたいと考えております。

　ボトルジャッキで仕事を理解　（前田さん）　　

前田さんは仕事の教材にとボトルジャッキに鉄板を溶接し、さらに人が乗れるようにベニヤ板を取り付けました。　これなら楽々と小さな力で静かに板を持ち上げることができます。板の上に乗っている人も板が上昇していることに全く気付かないくらいです。

装置の裏側はこのようになっています。	板は若干不安定なので胡坐をかいて座っています。
もちろん、手で床からの距離を測ると板が床から離れていくのが分かります。　小さな力での仕事が位置エネルギーに変わる教材にということですが、若干仕組みが複雑ですので、既習の生徒に紹介するのが無難でしょうか？
	板は若干不安定なので胡坐をかいて座っています。

　ブランコ　（前田さん）　　

世界一受けたい授業でアメリカの先生が行っていた実験を再現しました。加工した角材と紐でブランコを作ります。角材同士は接着剤やネジくぎ等の金物は使われておりません。
	この通り、角材と紐なわけですが。
梁に角材を引っ掛け、他の角材をはめていきます。不安定そうに見えますが、それが実験の面白さの根源になっています。
	角材ははめてあるだけ、スリルがあります。
飯田さんがチャレンジした予備実験では、角材が崩れてしまったため、軽量級の杉本さんが挑戦です。安全面も考えてヘルメットをかぶってもらいました。　下手に身動きは取れませんが、体を預けることができました。
	万が一のためヘルメットをかぶっての実験です。

　二酸化炭素サイフォン　（飯田さん）　　

ここしばらくサークルの話題になってきた「サイフォンの科学史」の鎖説を否定するには、水と違い分子間力が無視できる気体を使ったサイフォンを作ればということで、ドライアイスを使ったサイフォンの実験を追試してみました。　長さ2.5ｍ、内径1.5㎝のホースを用いて、ホースの出口、入り口の落差を１ｍにして実験です。
	レジ袋の中に入ったドライアイスが昇華し、二酸化炭素がホースを通ってサイフォンができるか確かめます。。
まず、袋とホースの隙間をなくし、袋内の気圧が高くなり、ロウソクの火が消えるのを確認します。このとき、でホース内が二酸化炭素で満たされています。　次に、袋を開放した状態で再び実験です。変わらず、ロウソクの火は消えます。二酸化炭素でもやはりサイフォンが実現しました。

袋の隙間を大体なくします。大雑把ですが本質的なのが飯田流！	火は消えました。確かにサイフォンができています。
さらに流速を調べるための実験です。空き缶にロウソクを立て、空き缶内に入ってくる二酸化炭素でロウソクが消えるまでの時間を測ります。二酸化炭素は空気の主成分（窒素、酸素）より密度が大きいため、　底から溜まっていくことを利用します。缶の底からロウソクまでの体積は1.5Ｌ。　では実験です。　　20秒ほどで火が消えました。πr²vt=Vよりv=0.42[m/s]となります。
	缶の底面積×ロウソクの高さで管内の二酸化炭素の体積を推定できます。

　仕事の原理を輪軸で！　（川田さん）　　

高校１年生の授業で輪軸の話をしたところ、生徒が輪軸を知らないようだったので、次の授業で作って見せることを約束した川田さん。生徒のニーズにすぐ答える、まさに教員の鏡ですね。　右の写真の通り、力×移動距離が一定になっているのをすぐ理解できますね。
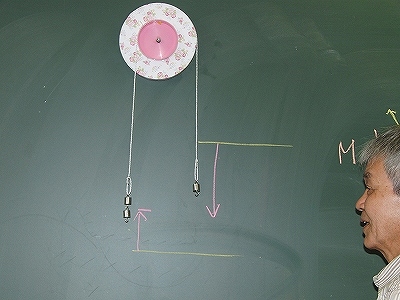	進む距離が２倍だと力は半分ですみます。

　簡単に作れる甘さ測定器　（川田さん）　　

中部大学の岡島茂樹さんの「甘さ測定器」を簡略化し、塩ビパイプなど安価な材料で作ってみました。1811年にフランスのアラゴにより発見された旋光現象ですが、「甘さ測定器」は、この現象を利用し、旋光率を調べることができます。


塩ビパイプにガラス板と偏光板が固定されています。	反対側には分度器と偏光板が付けられています。
まず、塩ビ管の溶液の上部になる空気層を通過する直線偏光した光が完全にカットされるように可動偏光板を回転させ、回転させた角度を分度器上の待ち針で読み取ります。次に、砂糖水を通過した光が完全にカットされる角度を読み、旋光角を測定します。
	偏光板の取り付けられた部分はこのように着脱でき、回転させることができます。
旋光率αを求めるには、　θ＝α・（ｌ/10）・Ｍ　（θ；旋光角[°]　ｌ；溶液の長さ[㎝]　Ｍ；溶液の濃度[g/㎝²] で計算できます。旋光を利用した糖度計　（川田さん）
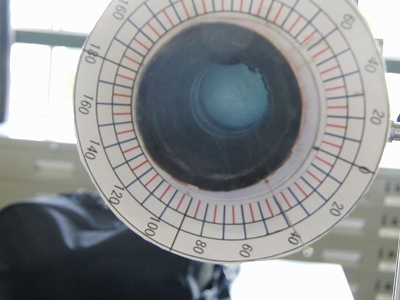	偏光板を回転させると明暗が変化します。

　続々・どっちが早い　（川田さん）　　

川田さんが学会に参加した際、とある教授が２点間を通過するのにかかる時間について、 ①　最短経路を進むのにかかる時間　と　②　鉛直方向に進んだのち水平に進むのにかかる時間　を比べるとどうなるかを語っていたようです。ここで、摩擦は無視でき、鉛直に落ちた後、なめらかに水平方向に進むこととします。どうなる思われますか？ア．　①の方が早いイ．　②の方が早いウ．　斜面の角度θによる
	教授は②の方が必ず早く着くと強弁していたそうですが。
結果は計算すれば分かりますね。36°＜θ＜90°の範囲では①の方が早くなります。よって、正解はウとなります。
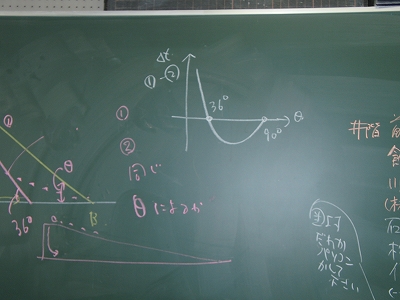	（①にかかる時間－②にかかる時間）はグラフのようになりました。

　　　　　[次ページヘ]