
2015年2月14日(土)愛知工業高校での例会の記録です。

2015年2月14日(土)愛知工業高校での例会の記録です。
| 加速する物体上でのヘリウム風船 (井階さん) |
| 前回、川田さんが紹介した生徒が考えた自動車内でのヘリウム風船の動きを定量的に扱いました。風船はダンボールの底から糸で固定しています。 まずは、水平面を加速して進む場合です。定滑車を用いて、一定の力で台車を引くことにより、等加速度運動を実現しました。 |
 |
| 定滑車を使い、おもりの重力で、等加速度運動を起こします。 | |
| 次は斜面での運動です。 斜面の角度は、鉛直方向と糸の下端からダンボールの上の端を結んだ直線がなす角度である13°としました。 これで、理論上、加速中は風船は左上端にいくはずです。 動きがかなり速いため、目視は正確性には欠けるかもしれませんが、風船が端に行ったような印象は残るでしょう。 |
 |
| ダンボールの左上端に風船が移動したように見えます。 |
| LEDを用いた内部光電効果とプランク定数の測定 (林さん) |
| LEDに光から十分なエネルギーが送られれば、物質内の電子が増加し、起電力が生じます。このような、物質内の電子が増加する現象は内部光電効果と呼ばれます。 |
 |
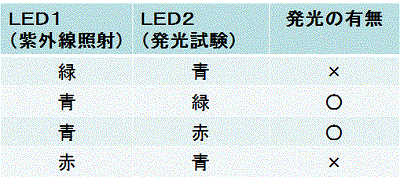
| この現象を確認するため、図のように2つのLEDを接続し(+は+、-は-に)、一方にの高い紫外線を照射します。このとき、もう一方のLEDが発光するか調べました。
結果は、右の表のとおりです。 このとき、青色LEDには2.3V、赤色には1Vほどの電圧が生じていましした。 赤を3つ直列につなげば、青が点くのではという意見が出て、実際やってみましたが、理由は分からないものの点きませんでした。 |
 |
| hν=eVからh=eV/νとなりますので、いくつかのLEDを使い各々の波長(λ=c/ν)でのエネルギーギャップの電圧eVを測れば、プランク定数を求めることができます。 林さんは ①照明の下でLEDの光が認識できなったとき と、 ②5μAの電流(定格の10-4がLEDに流れたとき とをデータを取り、グラフの傾きからプランク定数を求めると、①のときで、7.5×10-34、②で6.9×10-34(J・s)を得ました。 |
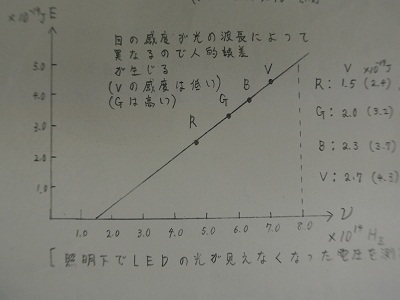 |
| グラフからプランク定数が求まります。 |
| 円運動と単振動(前田さん) |
| 単振動の速さを分かりやすく見せたいと装置を開発しました。 自転車の車輪に棒状のライトをつけます。これを回転させ、車輪を前後からみると、速さの上下成分が見えます。 |
 |
| 奥が円運動の確認用、手前のペンライトが鉛直成分の速さ用です。 | |
| 暗闇でやると、視覚刺激が減るため、ハーフミラーで反射させて見ると見やすいとのことでしたが、遠近法を頭が使ってしまい、棒の太さの変化が気になり、とても見やすいとはいえませんでした。 そこで、ハーフミラーを円筒形にしてみたところ、どの角度からも単振動の速さのごとく見えるようになりました。 |  |
| 円筒形にするのはナイスアイデアでした。 |
| 振動数を回転で見せる (前田さん) |
| 実際に車輪を回転させることで、周波数(振動数)が変化することを強く印象付けられます。 前田さんは直列共振の実験でも、車輪も同時に回転させ、周波数に比例して電流がたくさん流れるわけではなく、共振周波数付近のみ電流を増えることを強調しているそうです。 |  |
| 振動数の増減と共振周波数がとみに視覚的にも実感できます。 |
| 世界一簡単な構造で作られた電車 (前田さん) |
| youtubeで話題になっている「world's simplest train 」を作ってみました。 構造は軽い単5電池の両端にネオジム磁石を数個つけるだけです。コイル状にした導線にくぐらせると、磁石がゆっくり加速し進んでいきます。 そのユーモラスな動きを見ていると、いつの間にか「頑張れ!」と心の中で応援してしまうほどの愛くるしさがあります。 作るのは簡単そうに思えますが、導線はφ0.9のものが良いようで、φ1.6では動かなかったそうです。 また、磁石の向きは、同じ向きと考えてしまいがちですが、互いに逆向きにしなくてはいけません。 |
 |
| 簡単な構造ですが、作ってみて気付いたことも | |
| 環状にすると、電車はまわり続け、すごく面白いのですが、理屈が分からなければ「世界一簡単」なはずがありません。 仕組みをその場で川田さんが解説してくれました。 |
 |
| 川田さんの説明に納得しました。 | |
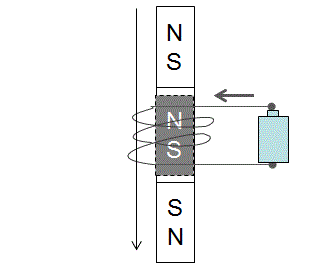 |
磁石をコイルの中に押し出してやると、磁石とコイルが接触することによって、コイルに電流が流れます。コイルを流れる電流により、磁場が生じ、ネオジム磁石と反発力が生じることによりさらに前方に電車を進ませます。 このことが連続的に起こることによって、電車はコイルがある限り、どんどん前に進んでいきます。 |
| 科教協東京大会DVD (鈴木さん) |
| 科教協夏の大会のまとめDVDがついに完成しました。 以前にもお知らせしたように、今までの紙媒体のものでなく、今回はデータになっており、動画等も収録されています。 大会発表の資料等も収録されており貴重な記録になりそうです。 |
 |
| これはダイヤモンドの燃焼の動画です。 |
| ゴムの伸び縮みと温度変化 (川田さん) |
| 理科教室に掲載されたゴムに関する記事ですが、川田さんはエントロピーを考慮すべきと自論を展開しました。 理科教室の記事では、ゴムを伸ばすと発熱し、ゴムを縮めるとき冷たくなるのを、ゴムを気体の分子運動のように扱い、熱力学第1法則⊿U = Q + W で、Q = 0 とし、外部から仕事をすれば、内部エネルギーが増加し、温度が上がると説明しています。 しかし、調べてみると培風館の「物理学辞典」には、「ゴム弾性について、ゴム弾性の本質は主にひずみによるエントロピー減少が原因であって、普通の固体弾性が内部エネルギーの変化に基づくのとまったく趣を異にする。」とあります。 |
 |
| 川田さんはエントロピーで考える重要性を説きました。 | |
| 議論が展開されましたが、結論は出なかったように思います。 |
| ベルヌーイの定理実験器 (川田さん) |
流体力学の重要な定理であるベルヌーイの定理の実験器を見つけ、購入しました。 ベルヌーイの定理は、P+ρgh+1/2ρV2=一定 と表されますが、 今回購入した実験器は、同じ高さなら流速Vが大きいほど、圧力Pが小さくなることを示すのに好都合であると考えられます。 管に水を流すと、理論的には真ん中の太い管が流速が遅くなり、圧力が大きくなるため、水位は上がると思われましたが、水位は左と変わりませんでした。 「これは困った。」ということで、塩ビパイプとジョイントで、装置をつくってみました。 |
 |
| これが、購入した教材です。 | |
 |
塩ビパイプは中が見えませんので、流体として空気を使い、出口に風船を付け、ブロワーで風を送ります。 すると、太い管は入り口から遠いにも関わらず、風船が大きく膨らみました。 これでめでたしめでたしと思いましたが、風船は大きいほど圧力が減る(吹き始めの方が圧力が大きい)ので、風船の大きさで圧力を説明するのはナンセンスだとか、風船も何度か膨らませると膨らみやすくなるとの声も出されました。 ところで、管を進む距離が長くなるにつれ流速が下がる原因ですが、川田さんは次式で与えられる圧力欠損ではないかと考えています。 ダルシ・ワイスバッハの式 ⊿P=λl/d×1/2ρV2 λ;管摩擦係数、l;管の間隔、d;管の直径 |
| 風船は分かりやすいですが、大きな問題も。 |