
2017年12月9日(土)明和高校での例会の記録です。

2017年12月9日(土)明和高校での例会の記録です。
| 入試問題あれこれ (前田さん) |
| 入試問題を解くだけでは味気ないと、入試問題に出てくるような実験装置の開発に勤しんでいる前田さん。次々と実験を紹介してくれました。 まずは、ループコースター落ちる・落ちない条件を考えさせます。 右の写真は、力学的エネルギー保存の法則の演示実験です。 前田さん曰く、年々、生徒が現象をイメージできなくなっているとか。確かに実感するものがあります。 |
 |
 |
| 円運動でのループコースター。 | 力学的エネルギー保存の法則の確認のための実験。 | |
| 続いて、摩擦がないとき、あるときの単振動の比較。台車だと摩擦が少なめです。 台車と金属製ばねはネオジウム磁石で着脱可能です。 |
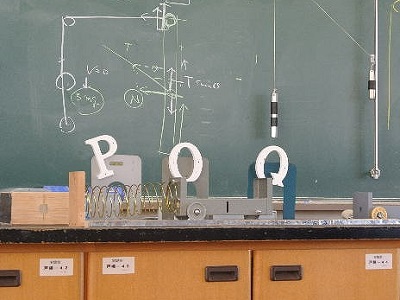 |
 |
| 後ろのOPQは点の場所を示すため! | 摩擦のあるときの単振動の演示用。 | |
| こちらは、単振動するばねからいつ物体が離れるかという問題の演示実験です。ばねの自然長(自重があるので正確には、縦に置いて静止する位置)で物体が離れるはずですが、スローで確認すると理屈通りにはいきませんでした。 |  |
|
| 物体がばねから離れる位置を示す実験。理論通りにはいきません。 |
| 屈折は速度変化 (石川さん) |
| 屈折の法則で波面が変化し、進行方向が変わることは生徒にはなかなか理解しにくい部分です。 石川さんは色によって速度が変化する車を自作しました。床の明るさを車の裏につけたLEDの反射光をCdSが拾い検出し、反射率によって無段階に速度が変化するものを開発しようと試みましたが、その場の明るさに影響を受けてしまうため、基準より明るいところと暗いところで、2段階で速度が2倍に変化するように仕様を変えました。 実演の様子です。右の写真をご覧ください。 白い紙の上では、両輪が等速で動くので、まっすぐに進みます。先に黒い紙の上に達した右側の車輪が速さが半分になり、左側の車輪との速度差で回転が生じます。少しすると、右側の車輪も速さが半分になり、両輪の速さが等しくなるため、再び直進します。 |
 |
|
| 黒い紙に入ると、直進していた車が曲がり始めます。 | ||
| さらに進むと、右側の車輪が白い紙に達するため、速くなり、再び回転が生じます。両輪が白紙に達すると、直進を再開! このときの角度は、はじめに白紙を進んでいたときと平行な方向に!と理屈通りの動きが観察でき、速度の変化が屈折を起こすことが一目瞭然!でした。 石川さんにとっては不本意な仕様変更だったかもしれませんが、実験の愉快さが最後の写真の参加者の表情から見て取れるでしょう。 |
 |
 |
| 両輪が黒い紙上にある間は、減速した速さで直進します。 | 黒い紙から出ると右の車輪のみ、元の速さに戻り、曲がります。 |
| かごの鳥 (奥村さん) |
| かごの中で鳥が羽ばたくと秤の目盛りはどうなるかといういわゆる「かごの鳥」。 では、モーターを選ぶなどなかなか教材作りになれていないと製作が困難です。 より手軽に実験することができないかと考え、5000円ほどで購入可能なドローン(25g)で実験を行ったところ、閉じられた段ボールの中では飛行時も質量の変化は生じず成功しました。 開いた空間では、奥村さん手持ちのスケールでは目盛りの変化が分かりませんでした。林ヒロさんによると目盛りの変化は10%程度だそうで、精密なスケールだと測定可能かもしれないので、今後実験を行う予定だそうです。 |
 |
| このかごの鳥が簡単に実現するかも! | |
| RLC直列回路 (成相さん) |
| いきわく1を参考にRLC直列回路を作ってみました。 発振器はアプリ「generator Pro」を使いアンプで増幅し、2つのコイルで昇圧します。1次コイルは100回、2次コイルは20000回巻いてあります。 この2次コイルに直列でコンデンサーにつなぎ、コイルの抵抗とでRLC直列回路になります。 抵抗がコンデンサーはアルミ板2枚、Cの調整は極板間の距離はラップの枚数で行います。ちなみに1枚では1000pF程度でした。一方、Lはコイルの鉄心を動かすことで調整可能です。 コンデンサー間のラップを1枚挟んだ状態では、380Hzで共振し、ラップの枚数を4倍、4枚にすると極板間隔が4倍になり、電気容量が1/4になるので、共振周波数が約2倍の800Hzになりました。 |
 |
|
| アルミ板の間隔をラップフィルムで調節します。 | ||
| 鉄心を置き、向きを変えることでコイルのインダクタンスを変化させ、蛍光灯を通る電流が変化することを確認します。 コイルのインダクタンスを変えなくても、電源の振動数を変えることで共振を起こさせることもできます。 |
 |
|
| 鉄心の置き方を変えることで蛍光灯の明るさが最大に!共振です。 |
| 電池式アンプ (杉本さん) |
| 退職されまたシニアボランティアに向かわれる杉本さん。現在、所属校がないため、実験器具が自由に使えません。そこでが実験用に安価で便利なアンプを探し、1.5Vの電池6本で駆動する電池式のアンプを購入しました。 これを成相さんの共振の実験で、使用してみましたが、実験が理屈通りにうまくいきません。 調べてみると、D級アンプというパルス幅を変調したアンプであることが分かりました。 このアンプだと、一定の50kHzにデジタル変調しパルス幅で音量をコントロールしているのため、LEDを低周波で発振しても、ついたままになってしまいます。 クントの実験等では十分使えます。 |
 |
 |
| 電源の必要がなく、持ち運びに便利な電池式のアンプです。 | ポータブルなクントの実験です。 |
| 宇宙空間はエイムズの部屋!(津山さん) |
| 杉本さんの担当した先進科学塾に参加した津山さん親子。 お嬢さんが、そこで製作したエイムズの部屋を改造し、夜空に浮かぶ星座の世界を作り出しました。 |
 |
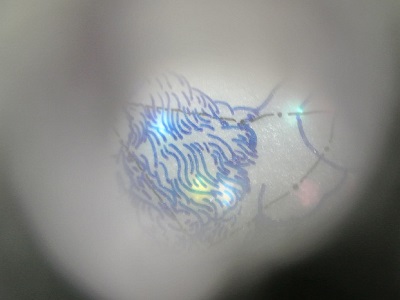 |
| 大人に囲まれ、恥ずかしかったでしょうが立派に発表してくれました。 | 牡牛座に煌めく星々。プラネタリウムのような世界が広がります。 | |
| 穴からのぞき込むと幻想的な星空が広がります。シートを追加すると、牡牛座の姿が浮かび上がります。 エイムズの部屋に、美的センスが加わり、魅力的な作品に仕上がりました。 |
 |
|
| 牡牛座の繊細な絵を投影しています。 |
| サイクロイド曲線 (川田さん) |
| 流体力学の「ベルヌーイの定理」を発見したダニエル・ベルヌーイはよく知られた存在ですが、このベルヌーイ家は17世紀から18世紀にかけて3代で8人の数学者を出した天才一家だったそうです。 1696年ヨハン・ベルヌーイは、「2点間を最も短い時間で移動する軌跡は?」という最速降下線(プラキスト・クローネ)問題を懸賞問題として出しました。 1晩で説いたという伝説があるニュートンをはじめ、ライプニッツ、ロピタル、ヨハンの兄で初めて数学者になったヤコブ・ベルヌーイの4人が正解したという、変分法誕生の契機になった問題でした。 なお、ガリレオは円弧と考え、間違いであったという逸話も残っています。 |
 |
| ベルヌーイ家の逸話を語る川田さん。 | |
| 4人の中でも、ヤコブは高度な数学は使わず、スネルの法則(高校でいう屈折の法則)を用いて、解き明かしました。 |
 |
| 斜面のサイクロイドです。 |
| 全身鏡(鈴木さん) |
| 「全身を映す鏡の大きさは最低どれだけか?」という中学校の教科書にも記載された問題です。 作図のように反射の法則を使い、頭のてっぺんと足の先からの光が目に入るように光線を作図すると背の高さの半分あればで事足りることが分かります。 鈴木さんは全身鏡を手に入れたのでこの実験を行ってみました。意外性を高める(?)ため、遠くでも必要な鏡の大きさは変わらないことを実演しようと、明和高校の長い廊下の端と端で実験を行いました。 ただ、これだけ遠いと鏡に写る像を確認するのが困難で、他人が観察するには被写体と鏡を結ぶ直線上に立たなくてはならず、確認は大変困難です。 |
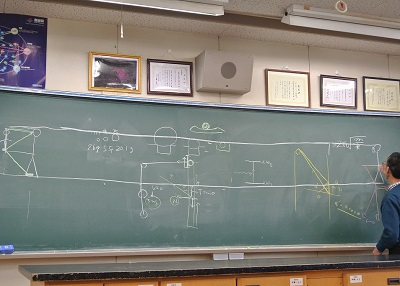 |
| 必要な鏡の大きさの説明です。 | |
| 鈴木さんはビデオカメラを使い、モニターを利用しましたが被写体の場所決めは困難を極めました。 最終的には、ビデオカメラで録画し、皆がモニターで確認することに! 何十mも遠くでやる意味があるのかという意見を始め、意外や意外!見せ方の検討がかなり必要ですね! |
 |
| 最後は映像を録画することにこれでも確認が大変です。 |