

学生読み物 打上花火の方程式 (PDF版527KB)
湘南台高校・山本明利


大輪の打上花火は、打ち上げ後最高点付近で「割薬」という火薬によって本体を炸裂させ、「星」と呼ばれる発光火薬を四方に散逸させます。これが輝
きながら花状に開くのが花火というわけです。発色はもちろん炎色反応によりま
す。これをグレーティングスクリーンを通してみると花火が7倍楽しめるのです が、その話はおいといて・・・
「星」はきれいに球形に広がるように見えます。一つ一つは放物線を描いているはずなのになぜ球形が崩れないのか不思議な気もします。そこで、次のような問題を考えてみることにします。同様の趣旨の入試問題をかつて見た記憶があり
ます。
====================================
問い:原点から等しい速さVで、四方八方へ一斉に投げ出された無数の質点は
どのような軌跡を描き、全体としてどのような運動をするか。それらが
通過する領域はどのような空間図形を作るか。
====================================
空気抵抗は考えず、重力のみが作用するとすれば、各質点の時刻tにおける座標はどの物理教科書にも載っているように
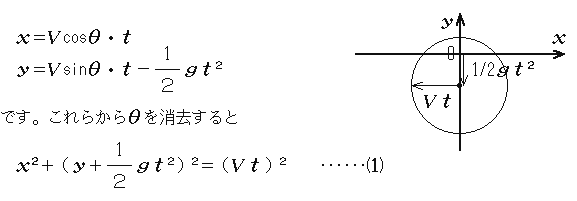
となります。つまりこれは半径がVtで中心の座標が(0,−1/2・gt2)であるような円の方程式(実際には球)です。等速で広がりつつ自由落下する球とい
うわけです。
あらゆる放物運動は、重力がない場合の初速度のみによる等速直線運動と、初速度0で重力のみによって起こる自由落下運動の合成として説明できることを思 い出すと、重力がない場合は無数の質点は原点を中心に一定の速さVで広がる球面を構成していますから、実際の運動はこれら球面をなす質点群をを一斉に自由 落下させたものになるわけです。これが「花火の運動」です。
さらに式(1)をt2についての二次方程式と見て、実根条件すなわち現実に起こりうるための条件を作ると、判別式より最終的に
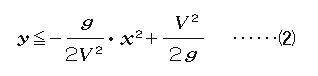
を得ます。これは頂点が

にあり、x軸との交点が

であるような上に凸な放物線(実際には回転放物面)の内部にあたります。
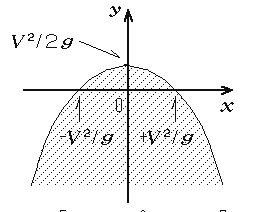
この曲面は、先の落下する球体の包絡面になっており、投げられた物体はその外部には決して出ることはできません。放物体を標的に当てようとする場合、標的がこの回転放物面の傘の内部になければ、どんな角度に放ってみても決して届 くことはないのです。
拡大図:空気抵抗がない場合の「等速で広がる球体の自由落下」のようすはここをクリック
さて、しだれ柳の花火の曲面はまさにこの領域を示すものだと考えられます。しだれ柳の「星」の火薬は四散する時に燃えながら軌跡を残すようになっているのでしょう。さらに、「しだれ」させて滞空時間を伸ばすために、しだれ柳の「星」にはそれぞれパラシュートがついているのだということです。パラシュートがなくても、「星」はいずれ空気抵抗により放物線を外れることになります。したがって実際には、上記の回転放物面の裾の方は円筒になるのです。その円筒の半径はどのようにして決まるでしょうか。また空気抵抗によって球形はゆがまないものでしょうか。
速度に比例する空気抵抗がある場合、各質点の時刻tにおける座標は、空気抵抗力をkmvとして(一般の空気抵抗係数をmで割ったものをkとしました)
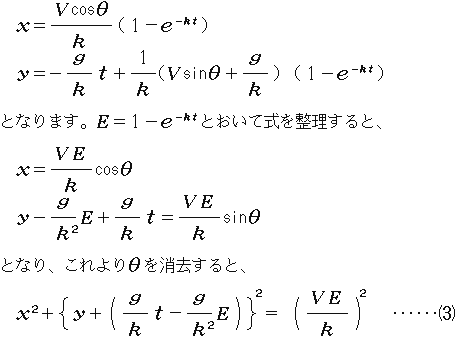
を得ます。
これは空気抵抗がない場合の式(1)に相当するものです。やはりy軸上を落下する円(球)の方程式になっていることがわかります。つまり、空気抵抗があっても花火の形は崩れないのです。
式(3)のパラメータEは時間の経過につれ0→1となるので、球の半径はV/k より広がることはありません。これが上で述べた回転放物面の裾の円筒の半径です。初速度Vで水平投射した放物体が最も遠くまで達しますが、そのx座標はV /kに漸近します。球の中心のy座標は十分時間が経つと、よく知られている終端速度g/kで落下することになります。

【参考文献】
「力学・改訂版」原島鮮著(裳華房)
Nifty Serve【理科の部屋】の以下に続くツリーの関連ログ
#11692 BYR10040 鵠沼 放物運動の1例 96/06/15
22:42