前の月の例会｜ 例会アルバム目次｜ 次の月の例会
例会速報 2022/02/20 Zoomによるオンラインミーティング
ＹＰＣホームページへ｜ 天神のページへ｜ 他のサークル・団体等へのリンク｜ 次回例会のご案内
授業研究：波動（物理基礎）の授業展開 勝田さんの発表
勝田さんは１年間の育休が明け、１月から現場に復帰した。物理基礎の波動を展開するにあたり、従来の波の基礎理論→音波という展開を見直し、音を基軸に授業を再構成した。以下、勝田さん自身のレポートを掲載する。
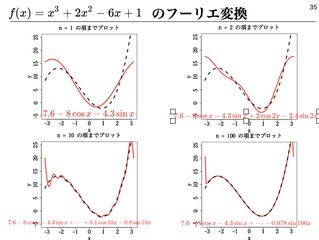
初回の授業で音、特に楽器の解析を目標に授業を進めていくことを提示した。毎回の授業冒頭で、解析したい音現象を提示し、そのために必要な波の知識を学んで応用、という展開を繰り返した。私物や音楽室から借りてきたものも含め、授業では多くの楽器を利用した。（左図）
また、フーリエ変換の考え方を早いうちに導入し、正弦波を学ぶ動機付けとした。フーリエ変換の考え方は、重ね合わせの原理との相性が抜群である。スペクトルの考え方を導入することで固有振動数を解析する意味が実感できるし、光との接続もよくなる。高校段階で数学的な基礎付けまではできないが、FFTアプリと組み合わせて、直感的な理解をえておくことは、大学進学後も役に立つと考える。
楽器の鳴る仕組みについては次のような展開をとった。まず、音の高さは振動数に対応するという既習事項を確認し、その後、「みんなは歌ったり楽器を演奏したりするとき１秒間に１００回とか１０００回も振動させてるの？」と発問し、そうではないことに気づかせる。
次に、「楽器を演奏する方法ってどんなものがある？」と訊き、「叩く・吹く・擦る・弾く」といった回答を拾う。そこで、「息を吹く」の入力を FFTにかけると、どこにもピークを持たない、全周波数が一様に重なった振動になることを確認する。全周波数が重なった音を、サウンドジェネレーターから出すと、ホワイトノイズになる。（右図）
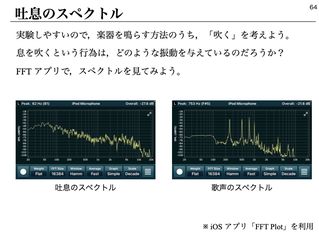
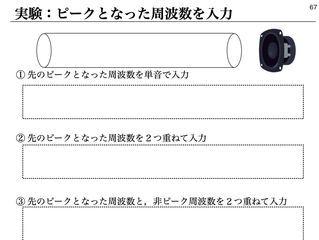
そこで、ホワイトノイズを Bluetooth スピーカーから出し、アクリルパイプの管口にあてると、音程のある音が鳴る。その音を FFTにかけると、複数のピークを持つ。そこで、そのピークとなった周波数の音を、単音としてスピーカーからだし、パイプの口に当てると、大きく共鳴する。さらに、ピークとなった音を複数重ね合わせても、共鳴する。また、ピークとなった周波数と、ピークではない周波数の音を重ねてパイプに入力すると、ピークとなった方の音だけが大きくなる。この実験は、FFTをリアルタイムに観察しながら演示することで、視覚的にもわかりやすくなる。（上図右）
先の実験により、共鳴する固有振動数の存在を認めることができる。さらに、フーリエ変換の知識を組み合わせれば、吹く・叩くといったすべての振動数の重ね合わせの入力に対し、楽器自身が固有振動数を選び出して共鳴することでスペクトルのピークが作られるという楽器の仕組みを理解できる。この展開をとることで、後に続く弦の固有振動、管（気柱）の固有振動の解析が、意味を持って実感できる。
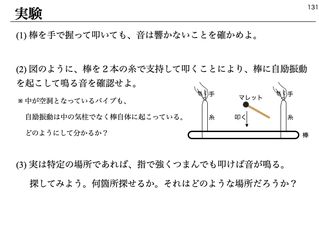
弦楽器の解析には、３時間を充てる。１時間めは、水糸におもりをつけて、滑車を通して吊るしたものを指で弾き、鳴る音を FFTにかけて、スペクトルのピークとなる振動数を記録する。
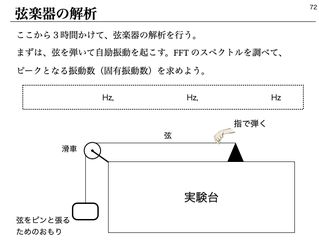
次に、発振器を利用して、先のピークとなった周波数で弦を揺らしてみると、大きく振動する点と、振動しない点が現れる。弦楽器の解析には、この振動を理解する必要がありそうだ。このことを動機づけに、ウェーブマシンで定常波を学ぶ。（左図）
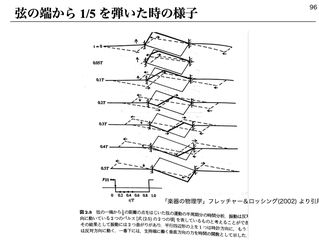
２時間目は、先に学んだ「定常波は、同じ形で逆向きに伝わる波が重なり合ってできる」という知識をもとに、「ギタリストって、両手で２か所を同時に弾いてる？」と発問し、そうではないことを確認する。そこで、各班にスリンキーを渡し、片側を固定した状態で、もう一端だけを動かしても定常波ができるか試させる。もちろんできる。このことから、どんなことが推論されるかを班で話し合わせ、「波が反射する」という考えを引き出す。その後、自由端／固定端反射、およびそれらによる定常波を学ぶ。
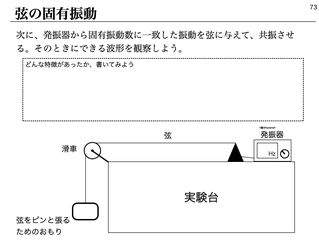
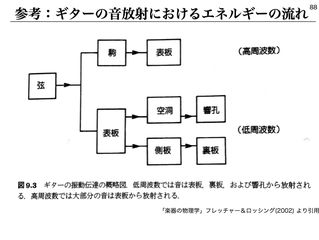
３時間目は、いよいよ実際の弦の固有振動数を求め、FFTの実験結果を再現できていることを確認する。また、音の高さを変えるにはどんな方法があるか？など、実際の楽器と、理論的に導出した結果を対比しながら確認していく。終わりには、実際の弦楽器にはより複雑な構造も多いが、少なくともスペクトルのピークを解析するという目的からは、ここで扱った理論モデルが適切であることを確認する。あくまで、解析したい現象のためのモデル、という立場である。なお、定常波の節となる位置を指定するハーモニクス奏法にも触れたいところだが、弦楽器のところでは扱わず、管楽器の後の打楽器の解析で扱った。（右図）
例会では質疑応答の際、「自励振動」についての議論が多かった。勝田は、非振動的な入力から（固有振動数の重ね合わせのような）振動を得るものは自励振動と教えていたが、参加者から自励振動はエネルギーの継続的な入力から振動を得るものだと指摘があった。後日に文献を読み直したところ、確かにそうっぽい。一方、この議論を受けてMLに西尾さんが流してくれた情報によると、文献によって定義がまちまちであることもわかった。この点は、もうちょっと勉強して、来年の授業では立場をはっきり示せるようになりたい。
静電誘導方式の静電気モーター 上橋さんの発表
ネット等で見かける静電気モーター(フランクリンモーター)は塩ビ棒等をティッシュ等でこすってマイナスに帯電させ、放電によって電荷を送る方式のものが多いが、上橋さんは6年前に「静電誘導方式の静電気モーター」を考案した。放電方式より電荷を送りやすく、夏場でも回転する。仕組みは電気盆を逆さまにしたものである。YpuTubeの動画はこちら。
作り方はスチロール板の真ん中にローターを取り付ける台を置き、左右にアルミホイルを貼り、アルミホイルからローター近くまで銅テープとアルミホイルで繋ぐ。ローターは百円ショップの蓋付きプラカップの中心に針を刺し、アルミテープを6枚貼る。針は上の磁石にくっつけ、下の磁石と針は3mm程度間隔をあけて宙づりにする。磁力で引っ張られるのでぶれずに回転する。
こするものは百円ショップのカードケースをカットしたものに、持ち手としてプラコップを貼る。カードケースは塩ビ製なので、アルミとの摩擦でマイナスに帯電する。
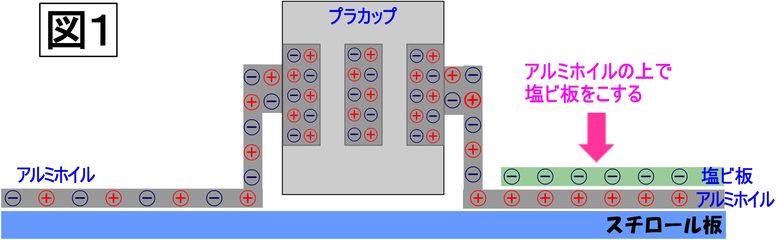
＜図１＞塩ビ板をアルミホイルの上でこすると、塩ビ板はマイナスにアルミホイルはプラスに帯電する。
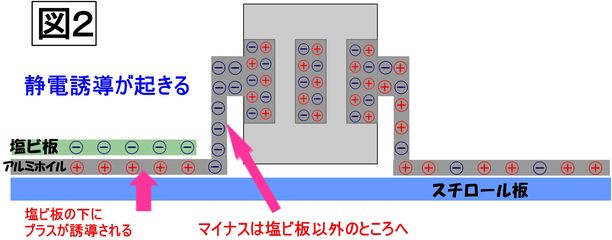
＜図２＞塩ビ板を右から左のアルミホイルの上に置き換えると塩ビ板の下のアルミホイルにはプラス電荷が誘導され、マイナス電荷は塩ビ板以外のところへ移動します。
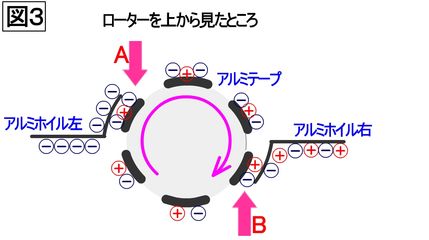＜図３＞ローターを上から見ると、A地点ではアルミホイル左からプラカップのアルミテープへマイナス電荷が送られ、マイナス同士の反発で回転を始める。B地点ではアルミテープからアルミホイル右へマイナス電荷が送られる。
（アルミホイル右は図1の摩擦によりプラスに帯電しているので、接地よりもマイナス電荷を送りやすい。）
塩ビ板を右から左へ、左から右へと移動させるだけで、以上の現象が繰り返され、ローターは回転を続ける。簡単に作ることが出来て、よく回るのでぜひ作ってみてほしい。
上橋さんの報告資料（PDFファイル：1.6MB）はここ。
ホッカイロとペットボトル 市原さんの発表
学校がコロナ対策でオンライン授業になったため、市原さんは家庭でできる実験として「ホッカイロの中身をペットボトルに入れて蓋を閉めるとどうなるだろうか」という課題を出した。内容的には中学の化学分野での出題である。ペットボトルが熱で変形するような気もするが、少なくとも500
mL程度の空気では、そこまで高温になるほどの酸素量がないため、温かくはなるのだが熱による変形は生じない。また、温度上昇に伴う体積膨張よりも、酸素の吸着の方が時間的には優位なようであり、ペットボトルが膨らむ様子もない。
実際にやってみるとペットボトルは凹む。質量保存の法則を信じて、アルキメデスの原理を疑わなければ、減少した気体の量を測定することができる。ペットボトルが542
mLであり、102 mLが減少量なので、19%弱となり、おそらく酸素の量と判断して問題ない値が出せた。
少し難しいが、ペットボトルの変形を維持したまま、火のついた線香を使って 中に酸素がないことを確認することもできる。「いろはす」や「Volvic」などの、やわらかい素材のペットボトルを使えば15分程度でほぼ変形が完了するので、授業時間内での演示も可能である。
％ や ppm は単位？ 西尾さんの発表
薬剤師国家試験では、％ や ppm が、m や kg などの物理量の単位と同じ「単位」として扱われている。Wikipediaでも「割合を示す単位」「無次元量単位」と説明されている。しかし、％
や ppm などは、「物理量＝数値×単位」の式に基づいて行われる単位換算などの計算では単なる数値として現れるものである。産業技術総合研究所計量標準総合センターのSIに関するパンフレット（SI国際文書第8版対応の2009年版）にある国際単位系(SI)FAQにも、「比率を示す
％ や ppm は単位ではありません。」とハッキリ書かれている。そして、「 ％ や ppm を用いる場合には、値を記述しようとする無次元量が何なのかを明確にする必要があります。」という大事な指摘もされている。
ただ、このSIに関するパンフレットの2019年版では、12個あるQ＆Aから、この ％ や ppm についてのものだけがなくなり、2019年のSI基本単位の改定に関するQ＆Aに置き換わっている。これは、2006年のSI国際文書第8版で「数学的記述において、国際的に認められている記号である
％（パーセント）は数字の0.01を表す。」と単なる数値であることが明記されていたものが2019年のSI国際文書第9版でなくなり、「国際的に認められている記号である
％（パーセント）は、SIと併用してよい。」という無次元量単位としての ％ や ppm を認めるかのような記述が入ってきたことが関係しているのだろう。
たしかに rad や sr のような無次元量単位はあるが、これらは明確に定義されたものである。それに対して、％ や ppm は文脈でいくらでも意味が変わる単なる割合の数値であって、本来の単位と同列に扱えるものではないことは確認したい。
なお、薬剤師国家試験では w/v％ という記号も単位として登場する。これは g/mL を百分率にして表したもので、異なる物理量の比の値であるから本来の
％ の概念ですらない。実用的に便利なために使われていて、薬学や化学の世界では必要な記号なのだろうが、量や単位の学習とは整合しない。
音色についてと音色に関わるパソコンアプリの紹介 古谷さんの発表
音色（ねいろ）についてはMLでも問題提起があったが、古谷さんは次の本を読んで自分なりに理解した内容を紹介してくれた。
本：日本音響学会「音のなんでも小辞典」ブルーバックス 2021年7月7日第29刷
以下、同書より抜粋。
「JISなどでは、大きさと高さが同じ2つの音が、違う音として聞こえるとき、その違いが、音色であるとしている。しかし、高さの違う音同士の音色は比較すらできないことになってちょっとおかしい」
「現在では、音色とは、ある音がその音であると聞こえる個性すべてを統合したもので、いわば音の全人格とでも考えた方がよいといわれている。」
「音色知覚の特徴は、多次元的な知覚にある。多くの研究によって音色知覚を説明するには少なくても三次元が必要であることが明らかになっている。逆に三次元あると、ある音の音色を大局的には表現可能であるという」
これらの三次元、ある音色を表すことばと対応させた研究によれば、「美しい」「快い」「澄んだ」などの”美しさ”を表す軸と「豊かな」「力強い」などの迫力を表す軸、「明るい」「華やかな」「キラキラした」などの”明るさ”や”甲高さ”を表す軸が見つかっている。このように、音色を表現することばには、なぜか視覚に関係したものが多い。
古谷さんによれば、電気製品や自動車の開発に上記のことを踏まえた研究がされているようである。
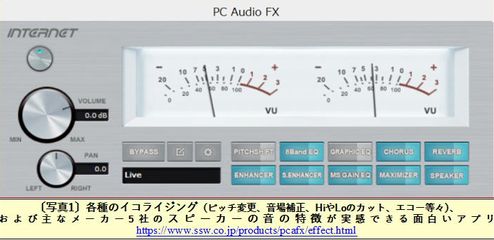
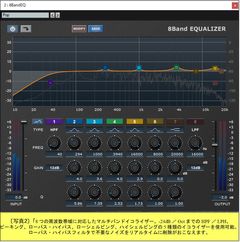
さらに、古谷さんは最近入手した「PC Audio FX」という音響アプリを紹介してくれた（画像上・左）。８バンドのイコライザと、各種スピーカーのシミュレータの組み合わせで、実際のオーディオセットの音を模擬できる。フランク永井の「低音の魅力」は高音域があってこそ引き立つのだという興味深い話もあった。
地震は予知できる？ 古谷さんの発表
古谷さんは数年前からメルマガ「週刊MEGA地震予測」に目を通している。最近その中に紹介されていた、村井俊治氏の考えや取り組んできた経過をまとめた動画を視聴し、彼の著書「地震は予測できる」（集英社新書）を読み、その内容を紹介してくれた。古谷さんによれば、第一にいわゆるGPS等の情報を利用しての国内各地の隆起と沈降を記録するという従来の地震研究にはなかった手法（特許取得）をとっていること。第二にミニプレート理論という日本列島を取り囲むプレートを細分化し、かつ実際に起こった地震との相関を調べるという方法に興味をもったというのが今回の紹介の動機だそうだ。
しかし、例会参加者からは、科学は学会等の場で正々堂々と議論されるべきで、これはまさに「ニセ科学」「トンデモ科学」の類いではないか（それもかなり巧妙な）との指摘があった。懐疑的な吟味も必要だろう。
Web上で見つけた昔YPCで紹介された音波ジェネレータ 天野さんの発表
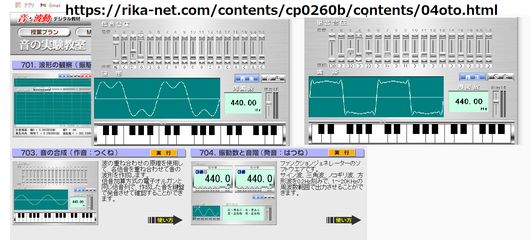WinXP時代（10年以上前）によく授業で活用されていた北村俊樹さん作の音源ソフト、「作音（つくね）」や「発音（はつね）」がWin10でも動作する状態でWeb上に公開されている。
理科ねっとわーく「音・波動デジタル教材/音の実験教室」
「作音・音の合成」は倍音合成を行うシンセサイザーで、正弦波を任意の振幅で合成する過程が実感できる。例えば基音に３倍音・５倍音・７倍音・・・のスライダーを１／3・1／5・1／7にして重ねていくと方形波に近づいていく。
「発音・振動数と音階」は独立した発振器を２チャンネル備えていて、うなりや和音の実験に使える。
シンプルで授業には使いやすいソフトである。教育フリーなので生徒に使わせるのにちょうどよい。
水流落下円柱の表面に生まれる模様を「定在波」としてとらえる 夏目さんの発表
水道の蛇口から落下する水流の振舞の中にもいろいろ奥の深い物理が含まれている。左の図のように、水流を細くしていくと、滑らかな流れがどこかで乱れて数珠状になって揺れ動く。これは古くから指摘されていて、ロゲルギスト「物理の散歩道」（岩波書店、1964年、p.110、高橋秀俊担当）には、右の図のように、数珠状の領域の動きが『増幅器』の働きとして紹介されている。さらに、ロゲルギスト「新
物理の散歩道・第４集」（ちくま学芸文庫、2009年、p.188）では、その数珠状のパターンを列の乱雑さと安定性の観点から議論している。
今回は、そのような「乱れの発生とその動き」ではなく、下の図のように鍋の底のような固い面に水流をぶつけた場合に、そこからの反動の働きで水流の表面に間隔1mm程度のかなり安定な縞模様が観察されることを報告する。実際、水流を鍋、コップ、洗面器などの底にあてて落下距離を数センチメートルにすると、間隔0.9mm～0.4mm程度の縞模様が3～8本程度出来る。もちろん、水流はどんどん落下しているが、この縞模様自体はかなり安定であって「定在波」のように見える。
さて、１月の例会で夏目さんは、ニュートンビーズ（鎖の噴水）に関連して、弾性波を伝えるヒモ状の媒体が高速で動く場合、媒体自体の動く速さｖと、発生する弾性波の伝わる速さuが一致すると、軌道の描く形状が止まっていてあたかも「定在波」のように見えることを報告した。
それを踏まえて夏目さんは、水道の蛇口から落下する水流の表面に発生する今回の縞模様についてもその「定在波」の見方をあてはめてみた。以下、夏目さんの説明を紹介する。
一般に、密度の異なる流体が、境界面を境に境界面と平行に動いていてその速さが異なる場合、境界面が不安定になる。これは各速さが一定（等速運動）の場合、ケルビン・ヘルムホルツ（KH）の不安定性として知られている。（参考文献の例はこちら）
そこで、今回の円柱形の水とその周囲の空気が円筒形の境界面をなす系をKH不安定性に適用してみた。予備的計算として、この不安定性で形成される限界波長λを求めると、水の表面張力γ、水の密度ρを用いて
λ=（2πγ）／（ρu２） (1)
と表される。ここで、uはその波（円筒面を表面張力で伝わる弾性波）の伝搬速度である。
次に、上で述べた「定在波」に見える条件としてこのuが波を伝搬させる媒質自体の速さｖで置き換えてみる。ニュートン力学で重力場（重力加速度ｇ）での自由落下においては、高さhだけ落下した物体の持つ速度vは
v2=2gh (2)
なので、この速度vと波の伝搬速度uを等しいと置くことにする。
u2=v2 (3)
以上、式(1),(2),(3)より、結果として
λh=（πγ）／（ρｇ） (4)
を得る。これは限界波長と高さが反比例関係にあることを意味している。ここへ各定数γ、ρ、gの値を代入するとλh=23mm2 である。これは観測された縞模様間隔0.9mm～0.4mmに対して、h=26mm～58mmを意味しており、不思議なほどよく合っている。
もちろん実際には、水流は重力場において等加速度運動をしており、速度は下へ行くほど大きくなっていると考えられる。それを取り込んだ理論的解析は今後の課題である。縞模様が下流へ行くほど間隔が狭くなっていることがうまく説明出来る可能性もある。
二次会 Zoomによるオンライン二次会
例会本体には40名が参加、二次会には14名の参加があった。このごろ、身近に感染者や濃厚接触者が出たという話をよく聞くようになって、コロナの流行のフェーズが変わってきていることを実感する。二次会でも三回目のワクチン接種のことがひとしきり話題になった。本日の例会発表で「音」に関するものが多かったが、二次会でも関連の話題で盛り上がった。物理屋には音楽好きが多いようだ。生徒も音楽に関心を示す者は多いので、「音」は生徒を物理にいざなうよい教材だと思われる。
ＹＰＣホームページへ｜ 天神のページへ｜ 他のサークル・団体等へのリンク｜ 次回例会のご案内
