前の月の例会｜ 例会アルバム目次｜ 次の月の例会
例会速報 2020/07/12 Zoomによるオンラインミーティング
ＹＰＣホームページへ｜ 天神のページへ｜ 他のサークル・団体等へのリンク｜ 次回例会のご案内
授業研究：長さの測定を通して有効数字を考える授業 勝田さんの発表
勝田さんは、４月からの休校期間中、授業動画を視聴した後に、Google Forms上で課題に取り組ませている。課題はその日の授業に結びつけた問題に加え、授業内容を自分の言葉でまとめたり、疑問点や感想も募っている。
その中で、例年になく「有効数字」についての質問や、授業で教えてほしいというコメントが多かった。分散登校が始まり、週に１度実験ができるようになったのを機に、測定を通して有効数字を考える授業に挑戦した。
大まかな方針は次の２つ。
①測定値には不確かさがある、ということを実感するために、測定を通して考えること
②考えてわかることと、「そういうルール」であることとの線引きをする。
まず、プリントに載せた長方形（右図）の、上辺と左辺の長さを測定する。但し、２種の定規で測定する。１つは、通常の 1mm 間隔目盛の定規。もう１つは、方眼紙に自分で書いて印刷した、1cm
間隔目盛の定規。
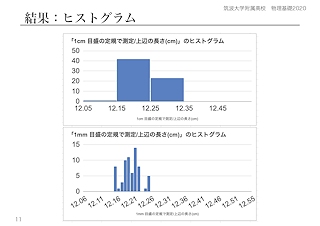
各自、長さを目盛の１桁下まで読み取って、スプレッドシートに値を入力してもらう。それをグラフ化すると（左図）、どちらもばらつきがあるのがわかるが、不確かな値が、1桁異なる。この事実をもとに、不確かさ、有効なのはどの「位」までなのかを考える。よく、「有効数字○桁」と言ってしまうが、実際に測定に伴う不確かさは、桁でなく位に現れる。
その後、科学的表記を導入する（右図）。現行の教育課程では、1年次の数学で統計を扱うので、平均や分散・標準偏差を用いた、11.72(3) cm
という表記法も導入できる。そして、「本当はこのような統計処理に基づくべきなんだけれど、限られた時間の中で毎回そんなことはやっていられないので・・・」と、有効数字に基づいた処理を考えていく。
まずは、和の計算（左図）。「長方形の周の長さを求めよ」という課題を課す。ただし、上辺は 1cm 目盛、左辺は 1mm 目盛の定規での測定値をそれぞれ採用する。
周の長さは「２×（上辺＋左辺）」でもとまるが、最初に出てくる「２」は測定値ではなく、不確かさはない。問題となるのはカッコの中の足し算である。筆算の形式で計算してみせ、不確かさが、「位」に基づいて決まることを確認する。その後の処理は、四捨五入である。筆算をしてみると、一見正当そうに見えるが、複数回足し算をしていったときの分散を考えれば、この考え方では不十分である。あくまで、「ルール」であることは明確に伝えた。
次に、積の計算（右図）。「長方形の面積を求めよ」という課題を課す。和のときと同様、筆算の形式で計算してみせると、今度は不確かさが、複数の桁へと伝播することがわかる。本来的には「桁」でも「位」でも考え方としては不十分なのだが、もともと不確かさのあった「桁」に基づいて決まると「信じる」ことにする。複数回の掛け算、繰り上がり・・・など、曖昧さは残るが、あくまでルールである。割り算ではより困ったことに、さらに平方根や三角関数など、本来は誤差伝播論に基づいて処理すべき量も、とりあえず高校理科では「桁」で処理して良いものとする、と伝えた。
授業後、勝田さんは全生徒に課題とともに「実は、教員になってから有効数字の授業を初めてしました.「そんなに気にしなくても・・・」「どうせ化学でやるし」くらいの認識だったんですが、実際授業やって良かったと思います？」という質問を投げかけた。するとたいへん好評であった。ひょっとすると、普段の物理の授業でも、ここまで好評だった回はないのでは・・・というくらいの好評ぶりだったという。
好評だった理由は、主に次の３つである。
・測定を通して不確かさを導入したので実感を伴う
・考えることと、ルールとして受け入れることを明示的に線引きした
・きちんと勉強したいときに、生徒がアクセスできるリソースが少ない（ネットにも）
オンライン例会での参加者からのコメントは、
・不確かさ、統計処理、有効数字は繋がっているけど、それぞれ異なる面もある
・JISなどの規格で有効数字の処理／あたいの丸め方は定まっている。そしてそれは高校理科で扱っている内容と異なる
・古くから（終わらない）議論が続いており、論文もたくさん出ている
・高校物理の生徒実験で、そこまで有効数字を気にするほどの精度の実験は少ない。実際には化学実験とかのほうが、まともに向き合う機会も多いかも？
・試験での有効数字処理ミスは減点するか？
・嫌いにならずに、興味を持って受け入れてもらうには？
など、議論が尽きないところであった。参加者も、皆さん有効数字の扱いには苦労している模様。
さらに勝田さん自身の感想。「今日の発表を受けて、夏目さんがノギスやモアレ縞の発表（下の記事を参照）を用意してくださったのも、たいへん嬉しかった。と、いうのも、私自身授業で扱っていて、共感できる部分が多かったからだ。」
参考文献（超オススメ！）：南茂夫他著「はじめての計測工学」のAmazonリンクはここ。
勝田さんの発表資料＆授業スライドのダウンロードはこちらから：https://www.evernote.com/l/AX5XgjgNDrlKFJUeV1Gnyj9nugucrJQwVnU
ポテトチップの袋のＳＥＭによる観察 永田さんの発表
ポテトチップの袋にはアルミニウムの膜が挟まれている。アルミニウムの膜は、酸素、水分、光を通しにくく、製品の保存に適している。6月の例会で、ポテトチップの袋に二本の画鋲を刺して導通テストをしたが、大きな抵抗しか得られなかった。この理由が分からないという問題提起があった。そこで永田さんは、袋の断面を自宅のSEM（走査型電子顕微鏡）で観察して構造を調べてみた。
左の画像は袋の断面SEM像であり、右の画像はその拡大像である。この結果から、約1.5μm厚さの非晶質に近いアルミ膜が樹脂の間に挟まれていることが分かった。
永田さんはさらに、ピンセットで膜を剥がすことを試みた。剥離を試みると、第一層、第二層が剥がれ、その下にアルミ面が見えた。そのアルミ面の導通を調べたところ、抵抗が０であった。第一層と二層の間には印刷層がある事が分かった。
読み取り精度をあげる方法としてノギス・モアレ・ウナリ効果 夏目さんの発表
夏目さんは、勝田さんの授業研究「誤差と有効数字」の基礎資料にノギスが載っていたことを受け、関連で、ノギスを使うことで測定精度があがる仕組みを紹介してくれた。それだけでは特殊な道具の説明に過ぎないが、実はモアレ模様、ウナリと言う重要なテーマの基礎原理とつながっている。以下、夏目さんの説明でそれを概観する。
ノギスには特に視覚を拡大する装置はない。しかし、長さの測定において有効数字が１桁あげるのに有効な貢献をする。それは、目盛と目盛の中間位置という判定しにくい状況を、目盛と目盛の一致という判定しやすい行為に替えることができるからである。
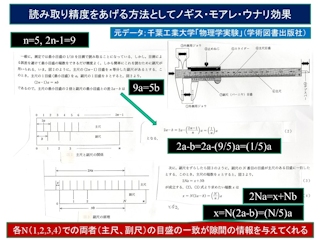
ノギスには左の図の右上に示したように主尺と副尺（バーニアと呼ぶ）がある。（左図をクリックで拡大。）式では、一般式を、主尺2n-1目盛を副尺でn等分する場合を議論してある。ここではn=5つまり主尺９単位が副尺5単位の場合を例として対応させてある。
主尺の目盛単位aと副尺の目盛単位ｂの間には(2n-1)a=nb（図中の式①）より2a-b=(1/n)a②の関係がある。物体の長さの測定により主尺から副尺をずらして副尺のN番目の目盛が主尺の目盛と一致したとすると、当然ズレxが生じて
2Na=x+Nb③となる。もしN=nならば②よりx=aとなってズレとは言えないので、Nは１からn-1の範囲になる。この条件下で③に②を代入するとx=N(2a-b)=(N/n)aを得る。これは、一致点Nを知るとxがaをn等分した長さのN倍と評価できることを意味している。図２に具体な例をn=5に即して描いてある。n=5の場合なので、主尺の単位目盛の間隔の1/5,2/5,3/5,4/5の点で主尺と副尺の目盛が一致して精度の高い測定ができる。
これは、４と９の最小公倍数が45であることを使っているとも言える。実際にこの2つの周期を右図のように縦縞模様として描いてみると、重なり方に長周期の構造が現れる。例えば黒棒と赤棒の重なりは45単位である。このような模様をモアレという。Webで「モアレ」と検索すると様々なパターンを見ることができる。
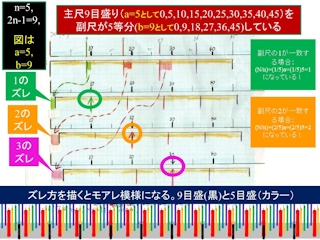
このモアレは2次元平面、３次元立体に拡張できる。
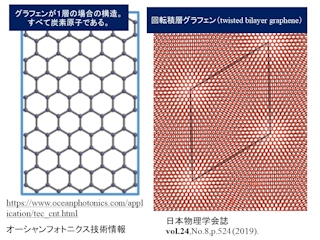
実際、結晶構造の場合、超格子を見つける手段になっている。結晶は同じ構造が並んでいる格子と呼ばれる周期構造を持っている。それよりさらに長い周期の構造を持つ場合に超格子という。石墨（グラファイト）は下左の図（クリックで拡大）の左側のように６角形を基本とするハチの巣格子が層状に並んでいる。その１枚をグラフェンと言う。このグラフェンを２枚重ねて２次元平面に超格子を作る試みは以前からあったが、最近わずか1～3度程度の回転で大きな超格子が作れることがわかった。2.65度の場合を同図の右側に示す。モアレ効果で超格子が明確にわかる。最先端の研究を垣間見ることができる。
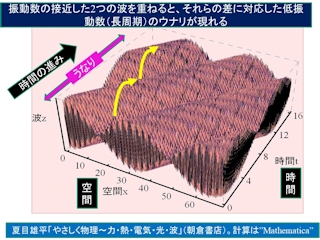
ここまでの説明は空間におけるモアレ現象であるが、時間の流れに拡張したものがウナリである。振動数f1と振動数f2の波を重ねると振動数がf1とf2の差に対応する新しい「振幅の高まり」が生まれる。下右の図に概要を示す。フルオーケストラの演奏中に（楽器が直接は出していない）予期しない低音がブワーっと出ることがある。これもウナリの現象である。
夏目さんの発表スライド資料（PDFファイル1.2MB）はここ。
干渉模様 天野さんの発表
生徒に自宅でもできる簡単な干渉の実験を紹介しようと予備実験をしていた天野さんは、CDやDVDにレーザー光線を当てていて、奇妙な干渉模様を見つけた。左はCDに斜めに当てたレーザーの反射光をスクリーンに映したところだ。トラック間隔による干渉縞（反射光の複数の光点）が上下に出ている。中央が０次、上下の弧状の光が1次の干渉光だ。
右のDVDだとトラックピッチが狭くなった分だけ干渉縞の間隔は広がり、一次の干渉光はずーっと上下に離れてしまい画面からははみ出している。スクリーン上に映っているのは0次の光点である。ところがこの光点がよく見ると直角方向の干渉パターンを伴っているのである。トラックピッチによる干渉縞は上下方向だからトラックに沿った方向の何らかの構造を反映しているに違いない。よく調べてみると、この現象はCDでも見られる。干渉縞の間隔が狭いということはより大きな構造を反映しているということだ。この縞の間隔は中心からの距離にも依存しているようだ。これは何を見ているのだろう。調べてみる価値がありそうだ。
v-tグラフの学習に陸上100m走のデータを利用 鈴木健夫さんの発表
ずいぶん昔の話だが、YPCの創始から数年後くらいに、大西さんの記事で、v-tグラフの学習で当時の100m走世界記録のカールルイスのデータを用いることが紹介された。鈴木さんもその後ずっとこれを授業で使っていた。2009年の世界陸上でウサインボルトが世界新を記録したときのデータもネットで公開されているので、それ以降はそのデータを使っている。（いまだに世界記録なので。）下の表がそのデータである。
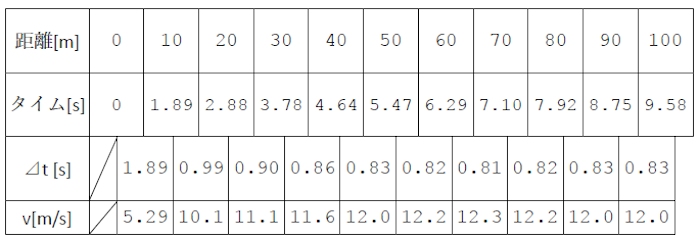
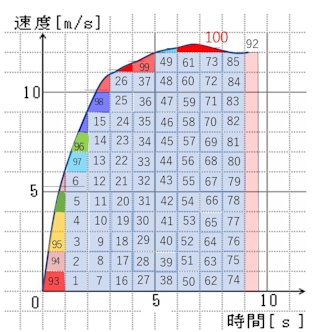生徒にはこれをグラフに描く作業をさせるが、鈴木さんは、最近は10m間の平均の速さは上記のように先に計算して表に示し、さらにはグラフにも横棒を描いて印刷したものを配っている。その上で、グラフになめらかな曲線を描かせて、さらにその面積を計算させる。計算と言うよりも、マス目を数える作業である。1マス1mの移動距離なので、100マスのはずである。中途半端なものは合わせて１マスになるものを数えていく。
鈴木さんは今回、生徒に作業させた後、それをパワーポイントで見せて理解させるようにした。左はカウントし終わった図である。途中の詳細や生徒用資料は以下のリンクを参照のこと。
鈴木さんの授業プリント（PDFファイル108KB）はここ。
鈴木さんの解説スライド（PDFファイル409KB）はここ。
YPCニュース46号の大西さんの記事（PDFファイル1.7MB）はここ。
YPCニュース51号の鈴木さんの記事（PDFファイル468KB）はここ。
シャボンアート 寺田さんの発表
寺田さんは、これまでジャンボシャボン玉アート広場という子どもイベントを開いてきた。シャボン膜の色の説明もし、その色の不思議をテーマに子どもへの見せ方を探ってきた。色鮮やかな膜や黒膜、白膜、透明膜の動きの不思議さに関心を持ち、子どもが実験したくなることを目指している。
例会では寺田さんが撮影し、YpuTubeに公開している美しいシャボンアートの動画の紹介があった。以下のURLからご覧いただける。
https://youtu.be/ZsRGa7dQ4c0
https://youtu.be/R1LxnQw3V58
https://youtu.be/S2FLGfhwl9g
https://youtu.be/TcK17h4t0jE
https://youtu.be/hbrveL1Wpbs
https://youtu.be/5NYyYHiLMcs
https://youtu.be/4oQmUbC31Lw
https://youtu.be/lvRbwT0RhHw
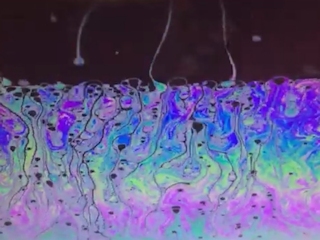
薄膜干渉の撮影のライティングは、例えば下の画像のようにする。できるだけムラのない広い光源を用意し、シャボン膜の表面で光が均等に反射するようにする。他の光はさえぎり、バックは黒くする。
■おまけの不思議な動画
塩ビ板にパンチであけた直径6ミリの穴にシャボン膜を張り、前回発表したタブレット虫メガネで撮影。つまり真下から見上げた小さなシャボン膜だ。小さいので表面張力が強く長持ちする。
https://youtu.be/vJJd2JFoBy8
飲み物がこぼれないドリンクホルダー？ 櫻井さんの発表
櫻井さんがカメラの前で演示してくれたのは、SpillNotという商品名のドリンクホルダー。上のストラップ部分に指を引っかけてぶら下げ、下のトレーにドリンク入りのグラスを載せると、かなり乱暴に揺らしても液面は常にトレーの面に平行に保たれ、ドリンクはこぼれない。うまくやればこぼさずに一回転させることもできる。パーティやアウトドア用のドリンクホルダーのようだが、非慣性系での慣性力などの物理教材として活用できないかと櫻井さんは考えている。国内では「こぼれないドリンクホルダー」としてAmazonなどでも扱いがあるようだ。
ちなみに、YPCでは古来この現象を「イスタンブールのお盆」（命名者は右近さん）と呼んでいる。その経緯は2003年4月例会に紹介されている。同様の応用例で有名なものに「郭公団子」がある。こちらは2004年8月例会で紹介された。
スマホスタビライザー 越さんの発表
越さんは、文化祭で動画制作をするので、便利なスマホスタビライザーを、試しに購入してみた。
手持ちで撮影しても、手振れを軽減させ、臨場感のある撮影ができる。10000円前後で様々な物がある。ジンバルともいわれるが、ジャイロは用いず、加速度センサーとサーボモーターでスマホを安定させるようだ。
関連して2次会での話題も報告しておく。スタビライザーを用いてスマホで撮影された「ドロステの果てで僕ら」という面白い映画の紹介があった。
1階のカフェと2階の自室の2台のカメラ付きモニターが2分の時差でつながっている。つまり、2分後の自分達と対話できる、という設定。2分後じゃ大した事は分からない、という事で2台のモニターを向い合わせてみると、モニターに映っている2分後のモニターには、更に2分後のモニターが...という事が無限に繰り返されていく(ドロステ効果とは、この様な効果をいう。詳しくはここ)。
話は演劇のノリで、どんどん大変な事態に！長回しのカメラワークと複雑な脚本で、面白く興味深い映画になっている。
金環日食と先月の部分日食 車田さんの発表
車田夫妻は2019年12月26日のグアム金環日食を見てきた。1月例会で時間切れで報告できず、その後コロナ騒ぎで延び延びになって半年後の報告となった。金環日食ツアーではなく個人旅行で行ってきたという。11月下旬にHISで探して、2人で約16万円格安だった。空港の北のグアムの主都ハガニア
の東の遠浅の Tamuning Bay のビーチで観測した。ちょうどクリスマス休暇にあたり、ビーチは閑散としていた。現地の人達は全く興味を示していなかったという。
カメラはカシオ HIGH SPEED EXILIM EX FH20。黒い紙を円筒形にして、先端に日食用の銀色のフィルム（ソーラーフィルター）を付けた筒を作りレンズにかぶせた。
第１接触から第３接触過ぎまでの写真。金環食は3分もあり、充分観望できたそうだ。
ピンホール板も用意した。金環の最中に撮影した影には、たくさんのファイアーリングが写っている。
車田さんからは、今年6月21日の部分日食に備えて、教材を準備した報告もあった。残念ながら当日は曇ってしまった。詳しくは車田さん自身のレポート（PDFファイル857KB）を参照してほしい。鏡の反射で部分日食を観察する方法を説明する動画（撮影：生徒、出演：車田さん）はこちら。→https://youtu.be/uQcN-06CZZg
新型コロナウイルスQ＆A 門倉さんの発表
門倉さんは、ある教科書会社より、新型コロナウイルスについて先生方が子どもたちに説明できるような資料を作成してほしいと依頼を受けた。対象は、小学校高学年から中学生程度がわかる内容という指定だった。生物は専門ではないので、最初は断ったが、専門家が書くと難しくなりすぎるので、中学校出身の方が中学生にはわかりやすく書けるということで、強引に押し切られて作成した。
東京大学医科学研究所感染・免疫部門ウイルス感染分野教授の河岡義裕氏・同准教授の今井正樹氏監の「猛威をふるう「ウイルス・感染症」にどう立ち向かうのか」という本と、厚生労働省、経済産業省、国立感染症研究所などから出ている通知やHPを確認しながら作成した。ウイルスとその予防に関する１４の質問に答える内容で作成し、PCR検査については専門的になりすぎると思い取り上げなかった。
取り上げた項目は左の図の１４項目。質問に対して、生徒向けの答えと、先生方向けの解説を示した。実は、ウイルスについては高校でも余り扱わず、免疫についても生物基礎で扱うだけだが、そのことも含めて、少し掘り下げた。特に注意したのは、除菌効果を謳っている薬品についてである。販売会社の損益につながる内容なので、余り強く否定することもできず、やんわりと解説をした。また、新型コロナウイルスについては、日々内容が変化しているため、その点も配慮した。教科書会社からは、著者や発行社名は伏せて、制作委員会として発行すると連絡が来た。
折しも、NHK特集の「人体シリーズ」でウイルスと免疫について取り上げていたので、それと併せて読むと理解が深まると思う。例会では、ウイルスは生物か無生物かという質問があったが、代謝機能を持たないため無生物という考えを専門家は強く持っているとのこと。従って、ウイルスを殺すという表現ではなく、不活化するという表現になるそうだ。
二次会Zoomによるオンライン二次会
二次会は17名が参加して、ドリンク持参でフランクな雰囲気で。文化祭の情報交換から始まって、白内障手術の記録動画視聴など、闘病情報の交換に発展。相応の年になれば病気や障害と二人三脚でうまくつきあいながら生きていくのである。若い会員にはまだ縁のない話ではあるが、人生やがてたどる道である。情報共有は大切だ。
越さんの映画紹介に関連して、「ドロステ効果」の実験も行った。Zoomに使用しているPCの外部カメラの向きを変えて、PCの画面を撮影すればよい。入れ子になった再帰的な画像が簡単に得られる。カメラを傾けると回転するような効果も楽しめる。
リアルでもオンラインでも変わらず、飲みながらも科学を楽しむYPCである。
ＹＰＣホームページへ｜ 天神のページへ｜ 他のサークル・団体等へのリンク｜ 次回例会のご案内
